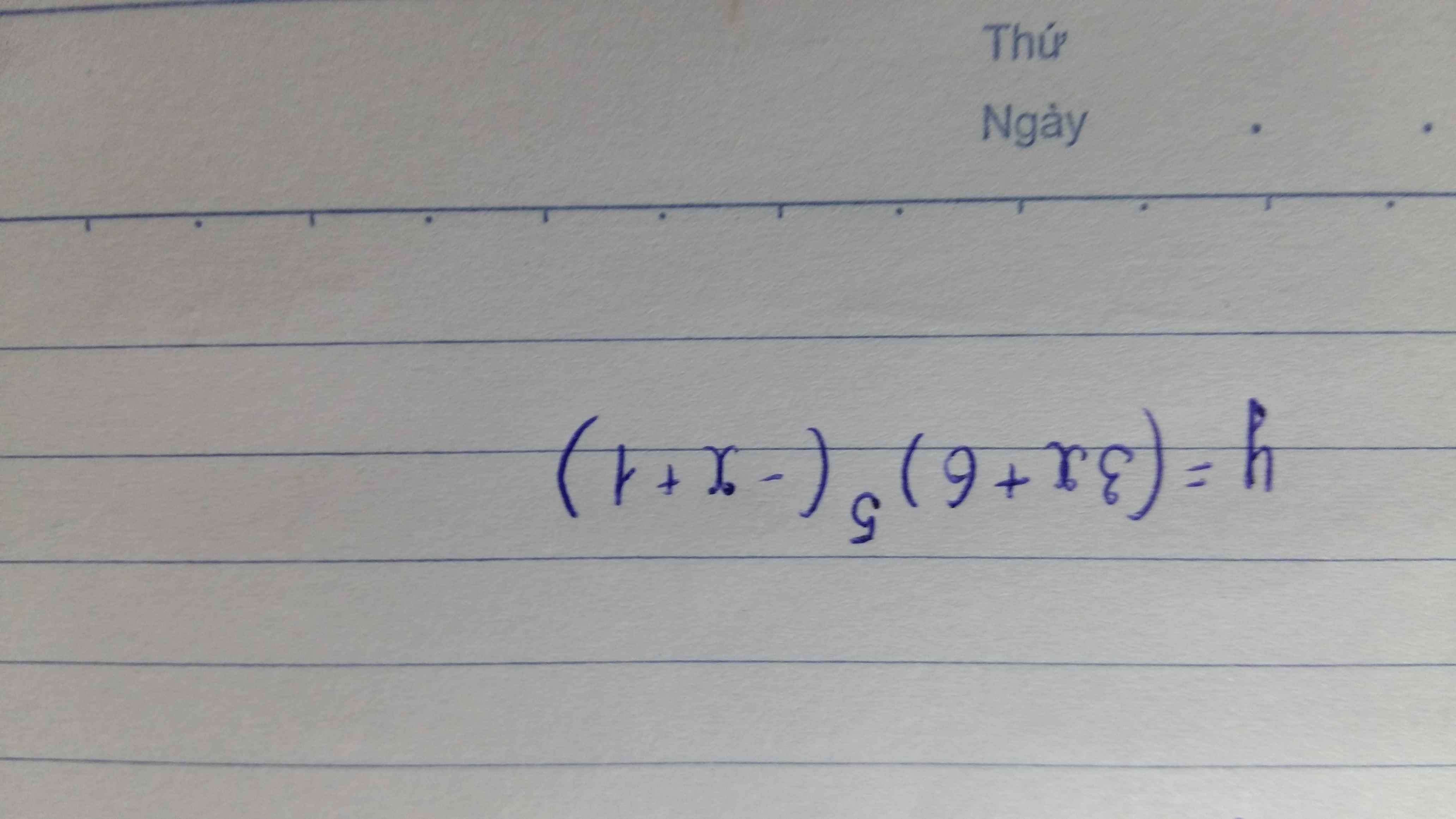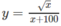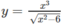Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(y'=4x^3-4x=4x\left(x^2-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu y' trên trục số:
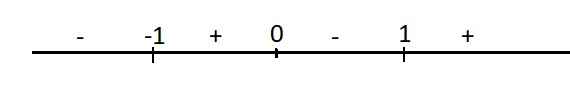
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
b.
\(y'=x^2+6x-7=0\Rightarrow\left[{}\begin{matrix}x=-7\\x=1\\\end{matrix}\right.\)
Dấu của y' trên trục số:
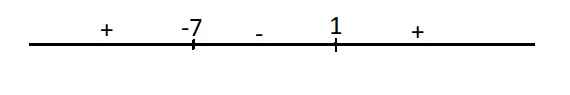
Hàm đồng biến trên các khoảng \(\left(-\infty;-7\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-7;1\right)\)

Xét hàm số:
y
=
4
-
x
2
x
+
3
m
TXĐ: R \ {−3m/2}
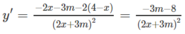
+) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng ![]()
+) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng
![]()
+) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4

\(y'=1-2.cosx.sinx=1-sin2x\le0,\forall x\)
Vậy hàm số nghịch biến trên R
Đạo hàm của hàm số y = x +` cos^2(x)`
Đạo hàm của x là 1
Đạo hàm của `cos^2(x) là -2sin(x)cos(x)` (sử dụng công thức đạo hàm của `cos^2(x)`).
Vậy, đạo hàm của hàm số y = x + `cos^2(x)` là `dy/dx = 1 - 2sin(x)cos(x).`
Khi `sin(x)cos(x) < 1/2`, tức là x thuộc khoảng `(0, π)` hoặc `(2π, 3π)`, ta có `1 - 2sin(x)cos(x) > 0.`
Khi `sin(x)cos(x) > 1/2`, tức là x thuộc khoảng `(π, 2π)`, ta có `1 - 2sin(x)cos(x) < 0.`
Vậy, trên các khoảng `(0, π)` và `(2π, 3π)`, đạo hàm là dương, và trên khoảng `(π, 2π)`, đạo hàm là âm.
Kết luận: hàm số y = x + `cos^2(x)` tăng trên các khoảng `(0, π)` và `(2π, 3π)`, và giảm trên khoảng `(π, 2π).`
Vậy, tính đơn điệu của hàm số y = x + `cos^2(x)` là tăng trên các khoảng `(0, π)` và `(2π, 3π)`, và giảm trên khoảng `(π, 2π).`

TXĐ: D=(\(-\infty;2\)]
\(y'=1+2.\dfrac{-1}{2\sqrt{2-x}}\)\(=1-\dfrac{1}{\sqrt{2-x}}\)
Ta có bảng biến thiên sau:
| x | \(-\infty\) 1 2 |
| y' | + 0 - || |
Vậy hàm số đồng biến trên khoảng \(\left(-\infty;1\right)\) và nghịch biến trên khoảng \(\left(1;2\right)\)

Lời giải:
$y=(3x+6)^5(-x+1)$
$y'=-9(3x+6)^4(2x-1)$
$y'=0\Leftrightarrow x=-2$ hoặc $x=\frac{1}{2}$
Lập BBT ta thấy hàm đồng biến trên $(-\infty; \frac{1}{2})$ và nghịch biến trên $(\frac{1}{2};+\infty)$

TXĐ: `D=RR`
`y'=x^3-4x`
`y'=0 <=>` \(\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
\(\begin{array}{|l|cr|} \hline x & -\infty & & -2 &&&& & 0 & &&&&2&&& & +\infty\\ \hline y' & &-& 0& & &+& &0& &&-&&0& &&+&\\ \hline\end{array}\)
Vậy hàm số đồng biến trên các khoảng: `(-2;0)` và `(2; +\infty)`
Hàm số nghịch biến trên các khoảng: `(-\infty; -2)` và `(0;2)`.

a) TXĐ: [0; +∞)
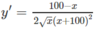
y’ = 0 ⇔ x = 100
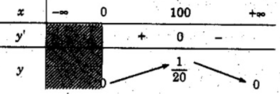
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; + ∞ )
b) TXĐ: ( - ∞ ; √6) ∪ (√6; + ∞ )
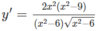
y’ = 0 ⇔ x = 3 hoặc x = -3

Vậy hàm số đồng biến trên các khoảng ( - ∞ ; -3), (3; + ∞ ), nghịch biến trên các khoảng (-3; −√6 − 6 ), (√6; 3).


cả nhà giúp mình với mai minh kiểm tra chất lượng rồi. Thanks all.