Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
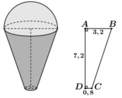
Gọi x và h lần lượt là bán kính và chiều cao của cốc, ta có x > 0 , 2 và
x − 0 , 2 2 h − 1 , 5 π = 180 ⇔ x − 0 , 2 2 = 180 h − 1 , 5 π với h = 15 c m .
Suy ra x = 0 , 2 + 40 3 π
Thể tích thủy tinh cần là:
V = π x 2 h = 180 = 60 , 717 c m 3 ⇒ T ≈ 30.000 đ ồ n g .

Đáp án A
Gọi x và h lần lượt là bán kính và chiều cao của cốc
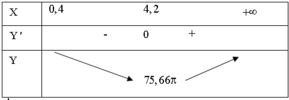
Ta có 0 , 4 < x và x − 0 , 2 2 h − 1 , 5 π = 480 π ⇔ h = 480 x − 0 , 2 2 + 1 , 5
Thể tích thủy tinh cần là V = π x 2 h − 480 π = x 2 480 x − 0 , 2 2 + 1 , 5 π − 480 π
⇒ V ' = 2 x x − 0 , 2 3 1 , 5 x − 0 , 2 3 − 480.0 , 2 π V ' = 0 ⇔ x = 480.0 , 2 1 , 5 3 + 0 , 2 = 4 , 2

Đáp án A
Gọi x và h lần lượt là bán kính đáy và chiều cao của cốc, ta có
0 , 4 < x và x − 0 , 2 2 h − 1 , 5 π = 480 π ⇔ h = 480 x − 0 , 2 2 + 1 , 5
Thể tích thủy tinh cần là: V = π x 2 h = 480 π = x 2 480 x − 0 , 2 2 + 1 , 5 − 480 π
⇒ V ' = 2 x x − 0 , 2 3 1 , 5 x − 0 , 2 3 − 480.0 , 2 π ; V ' = 0 ⇔ x = 480.0 , 2 1 , 5 3 + 0 , 2 = 4 , 2

Chọn đáp án C.

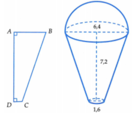
+) Thể tích khối tròn xoay sinh ra khi quay hình thang vuông ABCD quang trục AD là
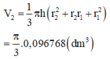
Do đó, lượng kem cần dùng để sản xuất một chiếc kem là


Thể tích của một chiếc kem cần tính bao gồm:
• Thể tích của hình nón cụt có lớn ![]()
Suy ra ![]()
Vậy thể tích của 1000 chiếc kem là: ![]()
Chọn B.

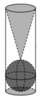
Gọi bán kính đáy của cốc hình trụ là R. Suy ra chiều cao của cốc nước hình trụ là 6R bán kính của viên bi là R; bán kính đáy hình nón là R; chiều cao của hình nón là 4R
Thể tích khối nón là ![]() Thể tích khối nón là
Thể tích khối nón là ![]()
Thể tích của cốc (thể tích lượng nước ban đầu) là ![]()
Suy ra thể tích nước còn lại: ![]() Vậy
Vậy 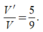
Chọn D.

Đáp án C
Chuẩn hóa bán kính của viên bi là 1 => Chiều cao của cốc là h = 2.
+) Thể tích của viên bi là V 1 = 4 π 3 . Gọi R, r lần lượt là bán kính của miệng cốc và đáy cốc.
+) Thể tích của cốc ( khối nón cụt ) là V 2 = πh 3 R 2 + R r + r 2 = 2 π 3 R 2 + R r + r 2
 +) Vì lượng nước tràn ra bằng nửa lượng nước đổ vào cốc
V
1
V
2
=
1
2
⇒
R
2
+
R
r
+
r
2
=
4
(
1
)
+) Vì lượng nước tràn ra bằng nửa lượng nước đổ vào cốc
V
1
V
2
=
1
2
⇒
R
2
+
R
r
+
r
2
=
4
(
1
)
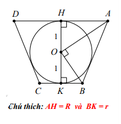
+) Xét mặt cắt của cốc khi thả viên bi vào trong cốc ( hình vẽ bên)
Dễ thấy ABCD là hình thang cân ⇒ O A 2 + O B 2 = A B 2 ( 2 )
Mà O A 2 = R 2 + 1 O B 2 = r 2 + 1 và A B 2 = A H - B K 2 + H K 2 = R - r 2 + 4 ( 3 )
Từ (2) và (3) ⇒ R 2 + r 2 + 2 = R - r 2 + 4 ⇔ R r = 1 ( 4 )
Từ (1) và (4) ⇒ R 2 + R r + r 2 = 4 R r ⇔ R r 2 = 3 R r + 1 = 0
⇔ R r = 3 + 5 2 . Vậy tỉ số cần tính là 3 + 5 2

Đáp án C.

Ta có
V b i = V m c = 4 3 h 2 3 . π ; V c o c = V n c = π 3 . h . R 2 + r 2 + R r
Mà V n c = 2 V m c do vậy π 3 h R 2 + r 2 + R r = 2. 4 3 . h 2 3 π
⇔ R 2 + r 2 + R . r = h 2
Mà ⇔ R 2 + r 2 + R . r = h 2 do vậy
P T ⇔ r R 2 − 3 r R + 1 = 0 ⇔ r R = 3 + 5 2 t m r R = 3 − 5 2 l
Vậy ta chọn C.


Đáp án B
Gọi x và h lần lượt là bán kính và chiều cao của cốc, ta có (x > 0,2) và