
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

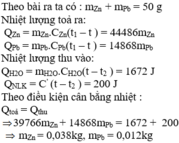

Nhiệt lượng toả ra :
Q = m 1 c 1 ∆ t + (0,05 - m1 ) c 2 ∆ t (1)
Ở đây m 1 , c 1 là khối lượng và nhiệt dung riêng của kẽm, c 2 là nhiệt dung riêng của chì.
Nhiệt lượng thu vào :
Q' = mc ∆ t' + c' ∆ t' = (mc + c') ∆ t' (2)
Ở đây m, c là khối lượng và nhiệt dung riêng của nước, c' là nhiệt dung riêng của nhiệt lượng kế.
Từ (1) và (2) rút ra :
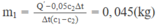
Khối lượng của chì m 2 = 0,05 – m 1 , hay m 2 = 0,005 kg.

Đáp án: B
Phương trình cân bằng nhiệt:
(Cnlk + mncn).(t – t1) = [mkck + (mhk – mk)cch].(t2 – t)
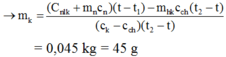
→ mch = mhk – mk = 5 g.

Gọi t1 là nhiệt độ ban đầu của miếng hợp kim, ta có t1=1360C
t2 là nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế, ta có t2=140C
t=180C - nhiệt độ khi cân bằng trong nhiệt lượng kế
Nhiệt lượng toả ra:
Q Z n = m Z n . C Z n ( t 1 − t ) Q P b = m P b . C P b ( t 1 − t ) ⇔ = m Z n .337. ( 136 − 18 ) = 39766 m Z n = m P b .126. ( 136 − 18 ) = 14868 m P b
Nhiệt lượng thu vào:
Q H 2 O = m H 2 O . C H 2 O ( t − t 2 ) = 100 1000 .4180 ( 18 − 14 ) = 1672 J Q N L K = C ' ( t − t 2 ) = 50. ( 18 − 14 ) = 200 J
Ta có, phương trình cân bằng nhiệt:
Q t o a = Q t h u ↔ 39766 m Z n + 14868 m P b = 1672 + 200 1
Mặt khác, theo đầu bài, ta có:
m Z n + m P b = 50 g = 0 , 05 k g 2
Từ (1) và (2), ta có:
39766 m Z n + 14868 m P b = 1872 m Z n + m P b = 0 , 05 → m Z n = 0 , 045 k g m P b = 4 , 67.10 − 3 ≈ 0 , 005 k g
Đáp án: A

Gọi t1 là nhiệt độ ban đầu của miếng hợp kim, ta có t1=1240C
t2 là nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế, ta có t2=160C
t=320C - nhiệt độ khi cân bằng trong nhiệt lượng kế
Nhiệt lượng toả ra:
Q Z n = m Z n . C Z n ( t 1 − t ) Q P b = m P b . C P b ( t 1 − t ) ⇔ = m Z n .337. ( 124 − 18 ) = 35722 m Z n = m P b .126. ( 124 − 18 ) = 13356 m P b
Nhiệt lượng thu vào:
Q H 2 O = m H 2 O . C H 2 O ( t − t 2 ) Q N L K = C ' ( t − t 2 ) ⇔ = 250 1000 .4180 ( 18 − 16 ) = 2090 J = 50. ( 18 − 16 ) = 100 J
Ta có, phương trình cân bằng nhiệt:
Q t o a = Q t h u ↔ 35722 m Z n + 13356 m P b = 2090 + 100 1
Mặt khác, theo đầu bài, ta có:
m Z n + m P b = 150 g = 0 , 15 k g 2
Từ (1) và (2), ta có:
35722 m Z n + 13356 m P b = 2190 m Z n + m P b = 0 , 15 → m Z n ≈ 8.10 − 3 k g m P b = 0 , 142 k g
Đáp án: A

Hướng dẫn giải.
Nhiệt lượng mà nhiệt lượng kế và nước thu vào :
Qthu = Q1 + Q2 = (m1c1 + m2c2)(t – t1).
Nhiệt lượng mà miếng kim loại tỏa ra :
Qtỏa = Q3 = m3c3. ∆t3 = m3c3 (t3 – t).
Trạng thái cân bằng nhiệt :
Q1 + Q2 = Q3.
⇔ (m1c1 + m2c2)(t – t1) = m3c3. ∆t3 = m3c3 (t3 – t).
=>
=>
=> c3 = 0,78.103 J/kg.K
Chúc bạn học tốt!![]()
Nhiệt lượng mà nhiệt lượng kế và nước hấp thụ
Q1 = ( 21,5 - 8,4 ) ( 0,128 . 0,128 .103 + 0,21 . 4200 )
= 13,1 . 898,384 = 11768,83 J
Nhiệt lượng do miếng kim loại tảo ra
Q2 = 0,192 . C ( 100 độ - 21,5 độ ) = 15,072C ( J )
Khi hệ thống cân bằng nhiệt ta có :
Q1 = Q2 ↔ 15,072C = 11768,83
→ C = 780 J/kg độ
Vậy nhiệt dung riêng của miếng kim loại là : C = 780 J / kg độ

Độ lớn của nhiệt lượng toả ra và nhiệt lượng thu vào :
Q t o ả = c 1 m 1 t 2 - t + c 2 m 2 t 2 - t = c 1 m 1 t 2 - t + c 2 M - m 1 t 2 - t (1)
Q t h u = c m t - t 1 + c 0 m 0 t - t (2)
Từ (1) và (2) dễ dàng tính được :
m 1 = 0,104 kg = 104 g ; m 2 = 0,046 kg = 46 g.

Nhiệt lượng thu vào của đồng thau và nước là
\( Q_{thu}=c_{Cu}m_{Cu}(t-8,4) +c_{nc}.m_{nc}.(t-8,4).(1) \)
Nhiệt lượng tỏa ra của miếng kim loại là
\( Q_{toa}=c_{kl}m_{kl}(100-t) .(2) \)
Khi hệ cân bằng nhiệt thì \(Q_{thu} = Q_{toa}\)
Thay số với nhiệt độ lúc cân bằng t = 21,5 độ C. Ta sẽ tính được nhiệt dung riêng của kim loại là
\(c_{kl} = \frac{0,128.0,128.10^3.13,1+0,21.4,18.10^3.13,1}{0,192.79} = 0,772.10^3\)(J/kg.K)

Bỏ qua sự truyền nhiệt ra môi trường bên ngoài. Nhiệt dung riêng của đồng thau là
0,128.103 J(kg.K).
Hướng dẫn giải.
Nhiệt lượng mà nhiệt lượng kế và nước thu vào :
Qthu = Q1 + Q2 = (m1c1 + m2c2)(t – t1).
Nhiệt lượng mà miếng kim loại tỏa ra :
Qtỏa = Q3 = m3c3. ∆t3 = m3c3 (t3 – t).
Trạng thái cân bằng nhiệt :
Q1 + Q2 = Q3.
⇔ (m1c1 + m2c2)(t – t1) = m3c3. ∆t3 = m3c3 (t3 – t).
\(\Rightarrow c_3=\dfrac{m_1c_1+m_2c_2\left(t-t_1\right)}{m_3\left(t_3-t\right)}\)
\(\Rightarrow c_3=\dfrac{\left(0,128.0,128+0,21.4,18\right).\left(21,5-8,4\right)10^3}{0,192.\left(100.21,5\right)}\)
=> c3 = 0,78.103 J/kg.K