Nghiệm phức có phần ảo dương của phương trình   z...">

Ưu đãi 1000 suất VIP đến hết ngày 9/9. Xem ngay!!!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
12 tháng 4 2019
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z )   z ¯ ...
Đọc tiếp

Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z )   z ¯ .
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
12 tháng 4 2019

Đúng(0)
PT
Pham Trong Bach
20 tháng 7 2019
Cho số phức z thỏa mãn z   ¯ = ( 2 + i ) 2   ( 1 - 2   i ) . Khi đó tổng bình phương phần thực và phần ảo của số phức z là A....
Đọc tiếp

Cho số phức z thỏa mãn z   ¯ = ( 2 + i ) 2   ( 1 - 2   i ) . Khi đó tổng bình phương phần thực và phần ảo của số phức z là
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
20 tháng 7 2019

Đáp án B

Đúng(0)
PT
Pham Trong Bach
1 tháng 12 2017
Nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 là z = a + bi, a,b ∈ R. Tính a+ 3 b A. 2 B. 1 C. –2 D. –1...
Đọc tiếp

Nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 là z = a + bi, a,b ∈ R. Tính a+ 3 b
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
1 tháng 12 2017

Đáp án A

Phương pháp :

Tìm nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 bằng MTCT.

Cách giải:

Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là

Đúng(0)
NH
Ngân Hoàng Xuân
2 tháng 4 2016

Tìm \(x\in Z\) để A thuộc Z và tìm giá trị đó

a) \(A=\frac{x+3}{x-2}\)

b)\(B=\frac{1-2x}{2+x}\)
#Hỏi cộng đồng OLM #Mẫu giáo
1
PN
Phạm Nguyễn Tất Đạt
2 tháng 4 2016

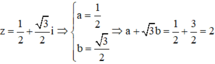
a)A=x+3/x-2

A=x-2+5/x-2

A=1+5/x-2

vì 1 thuộc Z nên để A thuộc Z thì 5 phải chia hết cho x-2

x-2 thuộc ước của 5

x-2 thuộc -5;-1;1;5

x = -3;1;3 hoặc 7

giá trị các biểu thức theo giá trị của x như trên và lần lượt là 0;-4;6;2

b)để B= 1-2x/2+x thuộc Z thì

1-2x phải chia hết cho 2+x

nên 1-2x-4+4  phải chia hết cho x+2

1-(2x+4)+4  phải chia hết cho x+2

1+4-[2(x+2]  phải chia hết cho x+2

5 -[2(x+2] phải chia hết cho x+2

vì [2(x+2] chia hết cho x+2 nên 5 phải chia hết cho x+2

suy ra x+2 thuộc ước của 5 

  x+2 thuộc -5;-1;1;5

x=-7;-3;-1;3

giá trị các biểu thức theo giá trị của x như trên và lần lượt là -3;-7;3;-1

Đúng(0)
DH
Đừng Hỏi Tên Tôi
19 tháng 4 2017

bạn làm sai 1 chút ở đầu

Đúng(0)
PT
Pham Trong Bach
23 tháng 6 2017
Cho số phức z thỏa mãn ( 2 − 3 i ) z + ( 4 + i ) z ¯ + ( 1 + 3 i ) 2 = 0 . Gọi a, b lần lượt là phần thực và phần ảo của số phức z. Khi đó 2 ...
Đọc tiếp

Cho số phức z thỏa mãn ( 2 − 3 i ) z + ( 4 + i ) z ¯ + ( 1 + 3 i ) 2 = 0 . Gọi a, b lần lượt là phần thực và phần ảo của số phức z. Khi đó 2 a   -   3 b  bằng
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
23 tháng 6 2017

Đáp án D

Đúng(0)
PT
Pham Trong Bach
29 tháng 6 2017
Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số...
Đọc tiếp

Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức w = z + 1 + i . Tính  P   =   a 2 + b 2

#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
29 tháng 6 2017

Ta có  2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i

Suy ra 

Chọn D. 

Đúng(0)
CC
cong chua gia bang
8 tháng 4 2016
tìm x,y,z biết : a) 3(x-2) - 4(2x+1) - 5(2x+3) = 50b) 312312 :( 4- 1/3 I 2x +1I = 21/22c) 3z-2y /37 = 5y- 3z / 15= 2z- 5x/2 va 10x -3y - 2z =...
Đọc tiếp

tìm x,y,z biết : 

a) 3(x-2) - 4(2x+1) - 5(2x+3) = 50

b) 312312 :( 4- 1/3 I 2x +1I = 21/22

c) 3z-2y /37 = 5y- 3z / 15= 2z- 5x/2 va 10x -3y - 2z = -4
#Hỏi cộng đồng OLM #Mẫu giáo
2
HP
Hoàng Phúc
8 tháng 4 2016

đăng hoài

Đúng(0)
PA
Phương An
7 tháng 5 2016

a) 3(x - 2) - 4(2x + 1) - 5(2x + 3) = 50

3x - 6 - 8x - 4 - 10x - 15 = 50

(3x - 8x - 10x) - (6 + 4 + 15) = 50

-15x + 25 = 50

-15x = 50 - 25

-15x = 25

x = 25 : (-15)

x = -5/3

Chúc bạn học tốtok

 

Đúng(0)
NN
Nguyễn Như Ý
1 tháng 2 2016

câu 1 :Gía trị x=1 có phải là nghiệm của phương trình hya không?Vì sao?

câu 2:Tìm điều kiện xác định của mỗi phương trình sau:

a)\(\frac{x}{x-1}\)=\(\frac{x+4}{x+1}\)

b)\(\frac{3}{x-2}\)=\(\frac{2x+3}{x-2}\)
#Hỏi cộng đồng OLM #Mẫu giáo
9
DM
Đặng Minh Triều
1 tháng 2 2016

a) ĐK: x-1 khác 0 và x+1 khác 0

<=> x khác 1 và x khác -1

b) ĐK: x-2 khác 0

<=> x khác 2

Đúng(0)
NN
Nguyễn Như Ý
1 tháng 2 2016

à thui câu 1 k cần lm lm hộ câu 2 nha

Đúng(0)
CC
cong chua gia bang
8 tháng 4 2016

tìm x,y,z biết : 

a) 3(x-2) - 4(2x+1) - 5(2x+3) = 50

b) \(3\frac{1}{2}\) :( 4- 1/3 I 2x +1I = 21/22

c) 3z-2y /37 = 5y- 3z / 15= 2z- 5x/2 va 10x -3y - 2z = -4
#Hỏi cộng đồng OLM #Mẫu giáo
2
HP
Hoàng Phúc
8 tháng 4 2016

3(x-2)-4(2x+1)-5(2x+3)=50

<=>(3x-6)-(8x+4)-(10x+15)=50

<=>3x-6-8x-4-10x-15=50

<=>(3x-8x-10x)+(-6-4-15)=50

<=>-15x-25=50

<=>-15x=75

<=>x=-5

Đúng(0)
HP
Hoàng Phúc
8 tháng 4 2016

\(3\frac{1}{2}:\left(4-\frac{1}{3}\left|2x+1\right|\right)=\frac{21}{22}\)

<=>\(4-\frac{1}{3}\left|2x+1\right|=\frac{7}{2}:\frac{21}{22}=\frac{11}{3}\)

<=>\(\frac{1}{3}\left|2x+1\right|=4-\frac{11}{3}=\frac{1}{3}\)

<=>\(\left|2x+1\right|=1\)

<=>2x+1=1 hoặc 2x+1=-1

<=>2x=0 hoặc 2x=-2

<=>x=0 hoặc x=-2

Vậy......................

Đúng(0)
PT
Pham Trong Bach
30 tháng 6 2017
Số nghiệm phức của phương trình  z + 2 | z | + 3 - i = ( 4 + i ) | z | ...
Đọc tiếp

Số nghiệm phức của phương trình  z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
30 tháng 6 2017

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Yêu cầu VIP