Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

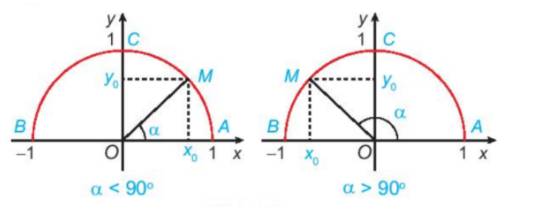
a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)
Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
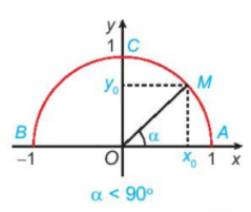
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)
Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.

a) Ta có: \(\left\{ \begin{array}{l}\sin {100^o} = \sin \left( {{{180}^o} - {{80}^o}} \right) = \sin {80^o}\\\cos {164^o} = \cos \left( {{{180}^o} - {{16}^o}} \right) = - \cos {16^o}\end{array} \right.\)
\( \Rightarrow \sin {100^o} + \sin {80^o} + \cos {16^o} + \cos {164^o}\)\( = \sin {80^o} + \sin {80^o} + \cos {16^o}-\cos {16^o}\)\( = 2\sin {80^o}.\)
b)
Ta có:
\(\left\{ \begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\quad ({0^o} < \alpha < {90^o})\)\( \Rightarrow 2\sin \left( {{{180}^o} - \alpha } \right).\cot \alpha - \cos \left( {{{180}^o} - \alpha } \right).\tan \alpha .\cot \left( {{{180}^o} - \alpha } \right)\) \( = 2\sin \alpha .\cot \alpha - \left( { - \cos \alpha } \right).\tan \alpha .\left( { - \cot \alpha } \right)\)\( = 2\sin \alpha .\cot \alpha - \cos \alpha .\tan \alpha .\cot \alpha \)
\( = 2\sin \alpha .\frac{{\cos \alpha }}{{\sin \alpha }} - \cos \alpha .\left( {\tan \alpha .\cot \alpha } \right)\)\( = 2\cos \alpha - \cos \alpha .1 = \cos \alpha .\)

a)\(sin^2\left(180^o-\alpha\right)+tan^2\left(180-\alpha\right).tan^2\left(270^o+\alpha\right)\)\(+sin\left(90^o+\alpha\right)cos\left(\alpha-360^o\right)\)
\(=sin^2\alpha+tan^2\alpha.cot^2\alpha+cos\alpha cos\alpha\)
\(=sin^2\alpha+cos^2\alpha+\left(tan\alpha cot\alpha\right)^2=1+1=2\).
\(\dfrac{cos\left(\alpha-180^o\right)}{sin\left(180^o-\alpha\right)}+\dfrac{tan\left(\alpha-180^o\right)cos\left(180^o+\alpha\right)sin\left(270^o+\alpha\right)}{tan\left(270^o+\alpha\right)}\)
\(=\dfrac{cos\left(180^o-\alpha\right)}{sin\left(180^o-\alpha\right)}+\dfrac{-tan\left(180^o-\alpha\right).cos\alpha.sin\left(90^o+\alpha\right)}{-tan\left(90^o+\alpha\right)}\)
\(=tan\left(180^o-\alpha\right)+\dfrac{tan\alpha.cos\alpha.cos\alpha}{cot\alpha}\)
\(=-tan\alpha+tan^2\alpha cos^2\alpha\)
\(=tan\alpha\left(-1+tan\alpha cos^2\alpha\right)\)
\(=tan\alpha\left(sin\alpha cos\alpha-1\right)\).

Tham khảo:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
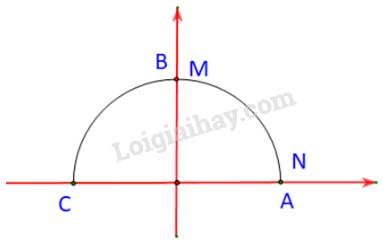
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
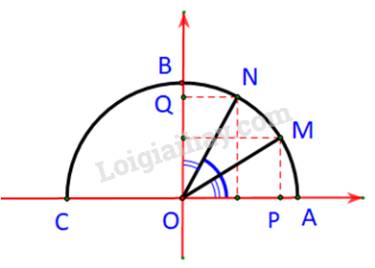
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)

Bạn xem lại biểu thức A. Biểu thức $A$ sau khi rút gọn thì \(A=\frac{-2\sin ^2a}{3\cos 2a}\) vẫn phụ thuộc vào $a$
------------
Sử dụng công thức: \(\sin (90-a)=\cos a; \cot (90-a)=\tan a\), ta có:
\(B=\tan ^260(\sin ^8a-\cos ^8a)+4\cos 60(\cos ^6a-\sin ^6a)-\cos ^6a(\tan ^2a-1)^3\)
\(=3(\sin ^8a-\cos ^8a)+2(\cos ^6a-\sin ^6a)-\cos ^6a\left(\frac{\sin ^2a}{\cos ^2a}-1\right)^3\)
\(=3(\sin ^8a-\cos ^8a)+2(\cos ^6a-\sin ^6a)-(\sin ^2a-\cos ^2a)^3\)
\(=3(\sin ^2a-\cos ^2a)(\sin ^2a+\cos ^2a)(\sin ^4a+\cos ^4a)+2(\cos ^2a-\sin ^2a)(\cos ^4a+\sin ^2a\cos ^2a+\sin ^4a)-(\sin ^2a-\cos ^2a)^3\)
\(=3(\sin ^2-\cos ^2a)(\sin ^4a+\cos ^4a)-2(\sin ^2a-\cos ^2a)(\cos ^4a+\sin ^2a\cos ^2a+\sin ^4a)-(\sin ^2a-\cos ^2a)^3\)
\(=(\sin ^2a-\cos ^2a)[3(\sin ^4a+\cos ^4a)-2(\cos ^4a+\sin ^2a\cos ^2a+\sin ^4a)-(\sin ^2a-\cos ^2a)^2]\)
\(=(\sin ^2a-\cos ^2a).0=0\). Do đó giá trị của biểu thức không phụ thuộc vào $a$
Cho sin = 1/3 với 90\(^o\)<\(\alpha\)<180\(^o\). Tính cos \(\alpha\) và tan (180\(^o\) - \(\alpha\))

\(90^0< a< 180^0\)
=>\(cosa< 0\)
\(sin^2a+cos^2a=1\)
=>\(cos^2a=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
mà cosa<0
nên \(cosa=-\dfrac{2\sqrt{2}}{3}\)
\(tan\left(180^0-a\right)=-tana=-\dfrac{sina}{cosa}\)
\(=-\dfrac{1}{3}:\dfrac{-2\sqrt{2}}{3}=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)

Tham khảo:
a)
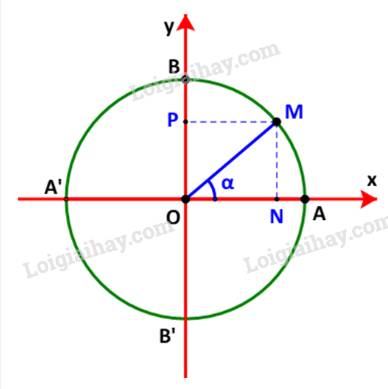
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM =1). (đpcm)
b)
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)
c)
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\)
\( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)

Mẫu số là \(-3cos2a\) hay \(-2cos2a\) vậy bạn? -3 không hợp lý
Tham khảo:
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc \(\alpha \) và \({180^o} - \alpha \).
Giả sử \(M\left( {{x_0};{y_o}} \right)\). Khi đó \(\cos \alpha = {x_0};\;\;\sin \alpha = {y_o}\)
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \(\alpha = {180^o} - \alpha = {90^o}\)
Tức là M và M’ lần lượt trùng nhau và trùng với B.
Và \(\left\{ \begin{array}{l}\cos \alpha = - \cos \left( {{{180}^o} - \alpha } \right) = 0;\\\sin \alpha = \sin \left( {{{180}^o} - \alpha } \right) = \sin {90^o} = 1.\\\cot \alpha = 0\end{array} \right.\)
Không tồn tại \(\tan \alpha \) với \(\alpha = {90^o}\)
Trường hợp 2: \(\alpha < {90^o} \Rightarrow {180^o} - \alpha > {90^o}\)
M nằm bên phải trục tung
M’ nằm bên trái trục tung
Dễ thấy: \(\widehat {M'OC} = {180^o} - \widehat {xOM'} = {180^o} - \left( {{{180}^o} - \alpha } \right) = \alpha = \widehat {xOM}\)
\( \Rightarrow \widehat {M'OB} = {90^o} - \widehat {M'OC} = {90^o} - \widehat {MOA} = \widehat {MOB}\)
Xét tam giác \(M'OB\) và tam giác \(MOB\) ta có:
\(OM = OM'\)
\(\widehat {M'OB} = \widehat {MOB}\)
OB chung
\(\begin{array}{l} \Rightarrow \Delta MOB = \Delta M'OB\\ \Rightarrow \left\{ \begin{array}{l}OM = OM'\\BM = BM'\end{array} \right.\end{array}\)
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(M'\left( { - {x_0};{y_o}} \right)\)
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Trường hợp 3: \(\alpha > {90^o} \Rightarrow {180^o} - \alpha < {90^o}\)
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Kết luận: Với mọi \({0^o} < \alpha < {180^o}\), ta luôn có
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha .\\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \;\;\;(\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array}\)