
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Nếu số thực x là một số thực thì môdun x chính là giá trị tuyệt đối của số phức z.
- Nếu số phức z không phải là một số thực thì chỉ có môdun của z, không có khái niệm giá trị tuyệt đối của z.


Mỗi số thực a là một số phức có phần ảo bằng 0.
Ta có: a ∈ R ⇒ a = a + 0i
Mô đun của số thực a là:
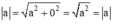
Như vậy với một số thực, khái niệm mô đun và khái niệm giá trị tuyệt đối là đồng nhất.

Bài 1: Thực hiện phép tính
a)136 - (2 . 52 + 23 . 3)
= 136 - (104 + 69)
= 136 - 173
= -37
b) (-243) + (-12) + (+243) + (-38) + (10)
= [(-243) + (+243)] + (-12) + (-38) + (10)
= 0 + (-40)
= -40
Bài 2 : Tìm x ∈ N, biết:
a) 6 . (x-81) = 54
⇒ x - 81 = 54 : 6
⇒ x - 81 = 9
x = 81 + 9
x = 90
Vậy : x = 90
b) 18 - (x-4) = 32
⇒ x - 4 = 18 - 32
⇒ x - 4 = -14
x = -14 + 4
x = -10

Đáp án B.
![]()
![]()
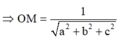
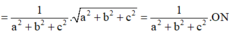
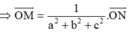
Suy ra

mặt khác M ∈ (P) nên ta được
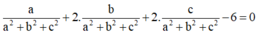
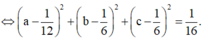
Vậy điểm N luôn thuộc mặt cầu có phương trình
x - 1 12 2 + y - 1 6 2 + z - 1 6 2 = 1 16
Kái n điểm thẳng hàngTrong hình học, n điểm được gọi là thẳng hàng nếu chúng nằm trên cùng một đường thẳng. Điều này có nghĩa là các điểm đó có thể được nối bằng một đường thẳng duy nhất mà không có điểm nào nằm ngoài đường thẳng đó.
Định lí về n điểm thẳng hàng (còn được gọi là định lí thẳng hàng) khẳng định rằng nếu có n điểm nằm trên cùng một đường thẳng, thì nếu ta chọn bất kỳ hai điểm trong số đó, thì đoạn thẳng nối hai điểm đó sẽ nằm hoàn toàn trên đường thẳng đó.