Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x+b\)
Thay x=2 và y=2 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot2=2\)
=>b+1=2
=>b=1
vậy: (d): \(y=\dfrac{1}{2}x+1\)
b: 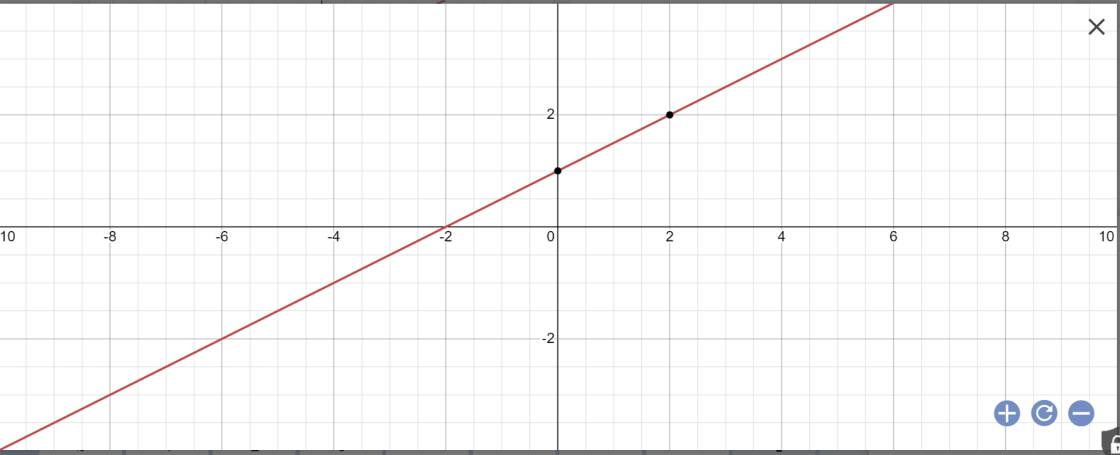
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
Ta có: (d): \(y=\dfrac{1}{2}x+1\)
=>a=1/2
=>\(tan\alpha=a=\dfrac{1}{2}\)
=>\(\alpha\simeq26^034'\)
d: tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)
Tọa độ C là;
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)
Vậy: B(-2;0); C(1;0)
\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)
\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)
Vì Ox\(\perp\)Oy nên OB\(\perp\)OC
=>ΔBOC vuông tại O
=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)

Lời giải:
a. ĐTHS đi qua $A(4;8)$ nên $y_A=ax_A+4$
$\Leftrightarrow 8=4a+4\Leftrightarrow a=1$
b. ĐTHS hàm số vừa tìm được là $y=x+4$
Với $x=0$ thì $y=0+4=4$. Ta có điểm $A(0;4)$
Với $x=1$ thì $y=1+4=5$. Ta có điểm $B(1;5)$
Nối $A,B$ ta có đths $y=x+4$

a) Đường thẳng d song song với đường thằng d'
=> \(\left\{{}\begin{matrix}a=12\\b\ne1\end{matrix}\right.\)
Thay x=2; y=-2, ta được:
\(-2=2.12+b\Rightarrow b=-26\)
P/s: Thấy đề nó sao sao, 12 to quá nhỉ:D?
b/ Vẽ tự vẽ nhé bạn.
c/ Gọi góc đó là \(\alpha\), ta có:
\(tg\alpha=\dfrac{26}{13}\)\(\Rightarrow\alpha=\)63o26'
d/ \(S_{OBC}=\dfrac{1}{2}OB.OC=\dfrac{1}{2}.26.13=169\left(cm^2\right)\)
Đúng đúng không ta;v?

- Gọi phương trình đường thẳng cần tìm có dạng : y = ax + b
- Thay tọa độ của điểm O và P và hàm số ta được hệ :
\(\left\{{}\begin{matrix}0a+b=0\\a\sqrt{3}+b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
=> Phương trình đường thẳng là : \(y=\dfrac{\sqrt{3}}{3}x\)
\(\Rightarrow Tan\alpha=a=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\alpha=30^o\)
Vậy ...

Ko bt đừng spam -.-
dcm đéo biết đừng trả lời, ngu còn gào mồm