
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

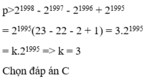

\(y=\dfrac{2x\left(x-1\right)-2}{x-1}=2x-\dfrac{2}{x-1}\)
tiêm cận y=2 x chia đồ thị thành hai nhánh
=> k< 2 PA(D)

a: \(A=\left(x-1\right)^2+2008\ge2008\)
Dấu '=' xảy ra khi x=1
d: \(D=\left|x+4\right|+1996\ge1996\forall x\)
Dấu '=' xảy ra khi x=-4

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.

Lời giải:
Ta có:
\((S): x^2+y^2+z^2-2x-2y-2z=0\)
\(\Leftrightarrow (x-1)^2+(y-1)^2+(z-1)^2=3\)
Do đó mặt cầu \((S)\) có tâm \(O=(1,1,1)\) và \(R=\sqrt{3}\)
Khi đó, dễ dàng nhận thấy \(A\in (S)\)
Ta có \(S_{OAB}=\frac{OA.OB.\sin \angle AOB}{2}\leq \frac{OA.OB.1}{2}=\frac{3}{2}\) vì \(\sin AOB\leq 1\)
Dấu bằng xảy ra khi \(\angle AOB=90^0\)

Viết lại bài toán cho dễ hiểu hơn: cho tứ diện MABC nội tiếp mặt cầu tâm \(I\left(-2;4;1\right)\) bán kính \(R=\sqrt{99}\), biết tam giác MBC vuông tại M và AM vuông góc mặt đáy, điểm \(M\left(1;7;-8\right)\) . Tìm điểm cố định mà (ABC) luôn đi qua
Với đề bài viết lại này, bài toán trở nên dễ đi 99%
Gọi P là trung điểm BC, qua P kẻ tia Px song song cùng chiều tia MA, trong mặt phẳng (AMP) qua trung điểm Q của AM kẻ đường thẳng song song MP cắt Px tại I \(\Rightarrow I\) là tâm mặt cầu
Gọi giao của AP và QI là N \(\Rightarrow N\) là trung điểm AP
Gọi giao của \(MI\) và \(AP\) là K \(\Rightarrow K\in\left(ABC\right)\)
Do A, N, K thẳng hàng, áp dụng định lý Menelaus cho tam giác IQM:
\(\frac{IK}{KM}.\frac{MA}{AQ}.\frac{QN}{NI}=1\Rightarrow\frac{IK}{KM}.\frac{2}{1}.\frac{1}{1}=1\Rightarrow KM=2IK\)
\(\Rightarrow\overrightarrow{KM}=2\overrightarrow{IK}\Rightarrow K\left(-1;5;-2\right)\Rightarrow P=11\)
sao mình không thể chọn điểm N thay vì điểm K v ạ có thể giải thích dùm e ko ạ tại hai điểm đó cùng năm trên 1 đt mà sao lấy K là điểm cố định thay vì N ấy ạ

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

Chọn D.
Phương trình đường thẳng d có hệ số góc k và đi qua I(1; 2) là d: y = k(x - 1) + 2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
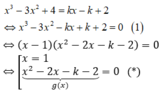
Để d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x1; x2 khác 1.
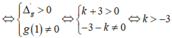
Hơn nữa theo Viet ta có

nên I là trung điểm AB.
Vậy chọn k > -3, hay k ∈ (-3;+∞).

Phương trình đường thẳng d; y=k(x-1)+2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
x3-3x2+4= k(x-1)+2. Hay x3-3x2-kx+k+2= 0 (1)
⇔
(
x
-
1
)
(
x
2
-
2
x
-
k
-
2
)
=
0
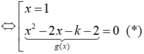
( C) cắt d tại ba điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt x1; x2 khác 1
⇔ ∆ ' g > 0 g ( 1 ) ≠ 0 ⇔ k + 3 > 0 - 3 - k ≠ 0 ⇔ k > - 3
Hơn nữa theo Viet ta có
x 1 + x 2 = 2 = 2 x I y 1 + y 2 = k ( x 1 + x 2 ) - 2 k + 4 = 4 = 2 y I
nên I là trung điểm AB.
Vậy chọn k> -3, hay k ∈ (-3; +∞). Do đó có vô số giá trị k nguyên thỏa mãn yêu cầu bài toán.
Chọn D.