Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

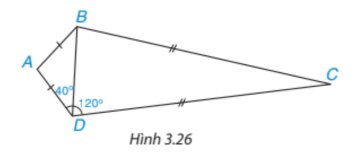
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

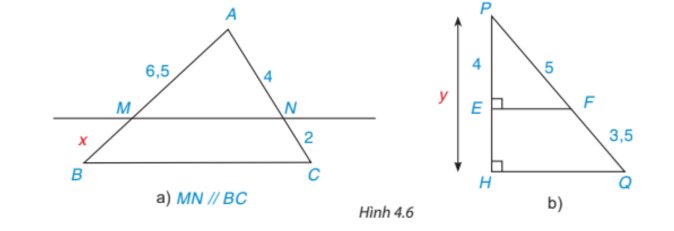
a)
Xét tam giác ABC có MN//BC
`=>(AM)/MB=(AN)/(NC)` (định lí thales)
`=>(6,5)/x=4/2`
`=>x=3,25`
b)
có QH⊥PH (hình vẽ)
FE⊥PH (hình vẽ)
Suy ra EF//HQ (từ vuông góc đến song song)
Xét tam giác PHQ có EF//HQ (cmt)
`=>(PE)/(PH)=(PF)/(PQ)` (định lí thales)
`=>4/x=5/(5+3,5)`
`=>4/x=5/(8,5)`
`=>x=6,8`

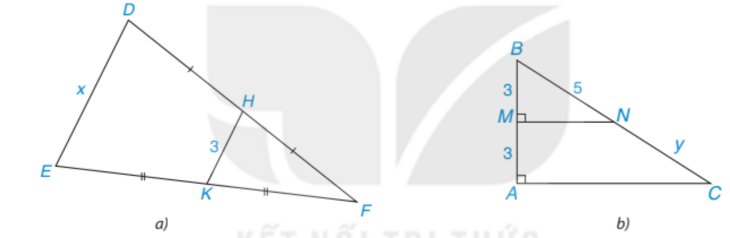
a. Do H, K lần lượt là trung điểm cạnh DF, EF
⇒ HK là đường trung bình của tam giác DEF.
⇒ DE = 2 HK = 2 \(\times\) 3 = 6.
b. Do M là trung điểm cạnh AB mà MN // AC (cùng vuông góc với AB)
⇒ MN là đường trung bình của tam giác ABC.
⇒ N là trung điểm của cạnh BC
⇒ y = NB = NC = 5.

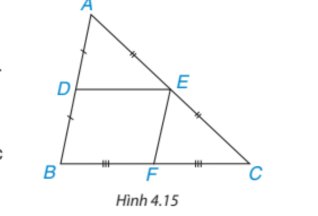
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)


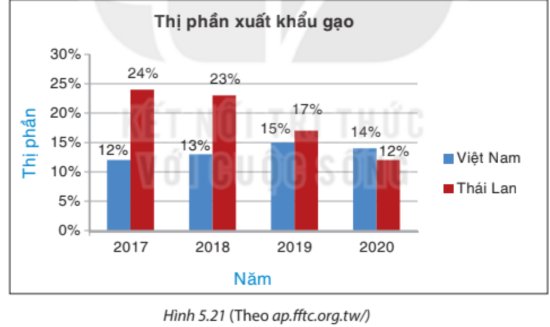
a) Thị phần xuất khẩu gạo của Thái Lan có xu thế giảm dần trong các năm từ 2017 đến 2020
b) Bảng thống kê thị phần xuất khẩu gạo của Việt Nam
Năm | 2017 | 2018 | 2019 | 2020 |
Tỉ lệ (%) | 12 | 13 | 15 | 14 |

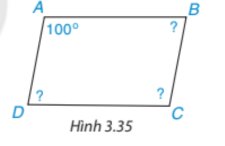
Vì ABCD là hình bình hành nên: \(\widehat A = \widehat C;\widehat B = \widehat D\) ta có:
\(\begin{array}{l}\widehat A = \widehat C = {100^o}\\\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\{100^o} + \widehat B + {100^o} + \widehat B = {360^o}\\2\widehat B + {200^o} = {360^o}\end{array}\)
Suy ra: \(2\widehat B = {360^o} - {200^o} = {160^o}\)
Do đó: \(\widehat B = {80^o}\) suy ra: \(\widehat B = \widehat D = {80^o}\)
Vậy các góc của hình bình hành ABCD là: \(\widehat A = {100^o};\widehat C = {100^o};\widehat B = {80^o};\widehat D = {80^o}\)

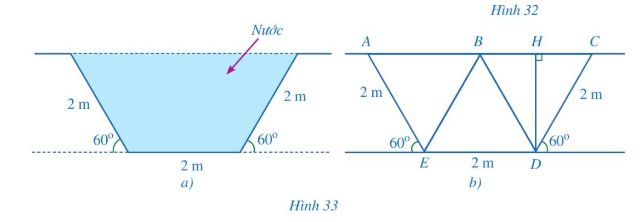
a, Do ACDE là hình thang cân nên
AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)
Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)
Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung
\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)
Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.
Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.
Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.
Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.
b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.
Suy ra AC = AB + BC = 4m.
Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.
Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)
Xét \(\Delta DHC\) vuông tại H ta có:
\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)
\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)
c, Diện tích hình thang cân AEDC là:
\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)
Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)






a) Hình này có 4 mặt bên
b) Diện tích của mỗi mặt bên là: \(4.5:2 = 10\) (\(c{m^2}\))
c) Diện tích của tất cả các mặt bên là: \(10.4 = 40\) (\(c{m^2}\))
d) Diện tích đáy là: \(4.4 = 16\) (\(c{m^2}\))