Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=16\)
hay AC=4cm
Xét ΔABC vuông tại A có
\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{ABC}\simeq53^0\)
\(\Leftrightarrow\widehat{ACB}=37^0\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBDC vuông tại B có AB là đường cao ứng với cạnh huyền CD, ta được:
\(BA^2=AC\cdot AD\)
\(\Leftrightarrow AD=\dfrac{3^2}{4}=2.25\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=3.75^2\)
hay BD=3,75cm
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AF là đường cao ứng với cạnh huyền BD, ta được:
\(BF\cdot BD=BA^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AE là đường cao ứng với cạnh huyền BC, ta được:
\(BE\cdot BC=BA^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(BF\cdot BD=BE\cdot BC\)

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=4,8cm
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{ACB}\simeq36^052'\)
b: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF đồng dạng với ΔACB
=>\(\widehat{AFE}=\widehat{ABC}\)

a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
=>AB^2=3,6*10=36
=>AB=6cm
Xét ΔABC vuông tại A có
sin ACB=AB/BC=3/5
=>góc ACB=37 độ
b: ΔABM vuông tại A có AK là đường cao
nên BK*BM=BA^2
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2
=>BK*BM=BH*BC
=>BK/BC=BH/BM
=>ΔBKH đồng dạng với ΔBCM
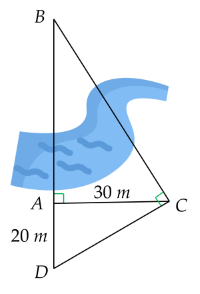
Xét ΔCBD vuông tại C có CA là đường cao
nên \(CA^2=AB\cdot AD\)
=>\(AB=\dfrac{30^2}{20}=\dfrac{900}{20}=45\left(m\right)\)
Xét ΔABC vuông tại A có \(tanACB=\dfrac{AB}{AC}=\dfrac{45}{30}=\dfrac{3}{2}\)
nên \(\widehat{ACB}\simeq56^018'\)