Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y, z lần lượt là số học sinh đạt loại giỏi một môn, hai môn và ba môn. Lập sơ đồ Ven liên hệ giữa các tập hợp, ta có hệ phương trình:
x + y + z = 45 − 7 x + 2 y + 3 z = 20 + 18 + 17 z = 5 ⇔ x = 26 y = 7 z = 5.
Vậy số học sinh đạt loại giỏi một môn là 26 em.
Đáp án B

Sơ đồ học sinh lớp 10A: 25 bạn 20 bạn 15 bạn 5 1 6 7
Số học sinh thích môn toán và tiếng anh và văn là:(25+15+20)-(5+7+1+6)=42(bạn)
Số học sinh không thích môn nào là:45-42=3(học sinh)
eh8 ihgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg

Số học sinh giỏi cả 3 hoặc không giỏi môn nào:
7+5=12(hs)
Tổng số hs giỏi chỉ một môn hoặc 2 trong 3 môn là:
45 - 12= 33(hs)
Số học sinh chỉ giỏi 1 môn
(20+17+18 - 5 x 3) - 33= 22 (học sinh)

Gọi A là tập hợp các học sinh của lớp 10A;
V là tập hợp các học sinh giỏi môn Văn và T là tập hợp các học sinh giỏi môn Toán của lớp 10A.
Kí hiệu |X| là số phần tử của tập hợp hữu hạn X.
Ta có

Đáp án D

Gọi A,B,C là tập hợp các học sinh tích môn toán , Văn , Anh
ta có :
\(\hept{\begin{cases}\left|A\right|=10,\left|B\right|=20,\left|C\right|=25\\\left|A\cap B\cap C\right|=3\\\left|A\cup B\cup C\right|=40\end{cases}}\) ta có : \(\left|A\cup B\cup C\right|=\left|A\right|+\left|B\right|+\left|C\right|-\left(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|\right)+\left|A\cap B\cap C\right|\)
nên \(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|=18\)
Do đó số học sinh chỉ thích đúng hai môn là :
\(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|-3\left|A\cap B\cap C\right|=18-3\times3=9\)

Đáp án B
Điểm trung bình môn ngoai ngữ của Hiếu khi kết thúc khóa học là:
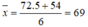
Điểm trung bình của bạn là: 6,9
khá fk a