Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi S là độ dài quãng đường AB
ta có thời gian xe đi nửa quãng đường đầu là :
\(\frac{S}{2}:20=\frac{S}{40}\)
ta có thời gian xe đi nửa quãng đường còn lại là :
\(\frac{S}{2}:30=\frac{S}{60}\)
Tổng thời gian xe đi trên đoạn đường AB là :
\(\frac{S}{40}+\frac{S}{60}=\frac{S}{24}\)
Vận tốc trung bình của xe trên đoạn đường AB là :
\(S:\frac{S}{24}=24\left(km\text{/h}\right)\)
bạn Trà My có làm được ko mà nói như đúng rồi vậy bạn

gọi t là thời gian xe di chuyển đến đền hùng
t1 là thời gian đi với vận tốc v1 = 90(km/h)
t2 là thời gian xe đi với vận tốc v2 = 60 (km/h)
theo đề ta có t1 = t2 =\(\frac{1}{2}t\)
Trong nửa thời gian đi thì xe đi được quãng đường là:
s1 = v1 . t1 = 90.\(\frac{1}{2}t=45t\left(km\right)\)
Trong thời gian còn lại xe đi được quãng đường là:
s2 = v2.t2 =60.\(\frac{1}{2}t=30t\left(km\right)\)
Vận tốc trung bình xe đi trên cả quãng đường là:
vtb = \(\frac{s_1+s_2}{t_1+t_2}=\frac{45t+30t}{t}=75\)(km/h)
Vậy vận tốc của xe là 75(km/h)

Gọi s là độ dài nửa quãng đường
Vận tốc trung bình trên cả quãng đường:
\(v_{tb}=\dfrac{2s}{t}=\dfrac{2s}{\dfrac{s}{40}+\dfrac{s}{30}}=\dfrac{2}{\dfrac{1}{40}+\dfrac{1}{30}}\approx34,29\left(\dfrac{km}{h}\right)\)

Gọi S(km) là độ dài quãng đường (S>0)
\(\left\{{}\begin{matrix}t_1=\dfrac{\dfrac{S}{2}}{v_1}=\dfrac{S}{2.4}=\dfrac{S}{8}\left(h\right)\\t_2=\dfrac{\dfrac{S}{2}}{v_2}=\dfrac{S}{2.6}=\dfrac{S}{12}\left(h\right)\end{matrix}\right.\)
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{8}+\dfrac{S}{12}}=\dfrac{S}{\dfrac{5}{24}S}=\dfrac{24}{5}=4,8\left(km/h\right)\)

Tự tóm tắt
______________
Giải:
Vận tốc trung bình của xe trên cả quãng đường là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}\)
\(\Leftrightarrow v_{tb}=\dfrac{\dfrac{1}{2}s+\dfrac{1}{2}s}{\dfrac{s_1}{v_1}+\dfrac{s_2}{v_2}}\)
\(\Leftrightarrow v_{tb}=\dfrac{\dfrac{1}{2}s+\dfrac{1}{2}s}{\dfrac{\dfrac{1}{2}s}{v_1}+\dfrac{\dfrac{1}{2}s}{v_2}}\)
\(\Leftrightarrow v_{tb}=\dfrac{s}{\dfrac{1}{2}s\left(\dfrac{1}{v_1}+\dfrac{1}{v_2}\right)}\)
\(\Leftrightarrow v_{tb}=\dfrac{s}{s\left(\dfrac{1}{2v_1}+\dfrac{1}{2v_2}\right)}\)
\(\Leftrightarrow v_{tb}=\dfrac{1}{\dfrac{1}{2v_1}+\dfrac{1}{2v_2}}\)
\(\Leftrightarrow v_{tb}=\dfrac{1}{\dfrac{1}{2.30}+\dfrac{1}{2.60}}=\dfrac{1}{\dfrac{1}{60}+\dfrac{1}{120}}=40\left(km/h\right)\)
Vậy ...

\(v_{tb}=\dfrac{s}{\dfrac{\dfrac{1}{2}s}{v'}+\dfrac{\dfrac{1}{2}s}{v''}}=\dfrac{s}{\dfrac{s}{20}+\dfrac{s}{15}}=\dfrac{s}{\dfrac{7s}{60}}=\dfrac{60}{7}\approx8,6\left(\dfrac{km}{h}\right)\)
Thời gian xe đi nửa quãng đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{S}{2}}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{2\cdot20}=\dfrac{S}{40}\left(h\right)\)
Thời gian xe đi trên nửa quãng đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{\dfrac{S}{2}}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{2\cdot15}=\dfrac{S}{30}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{30}}=\dfrac{S}{\dfrac{7S}{120}}=\dfrac{120}{7}\approx17,14\)km/h
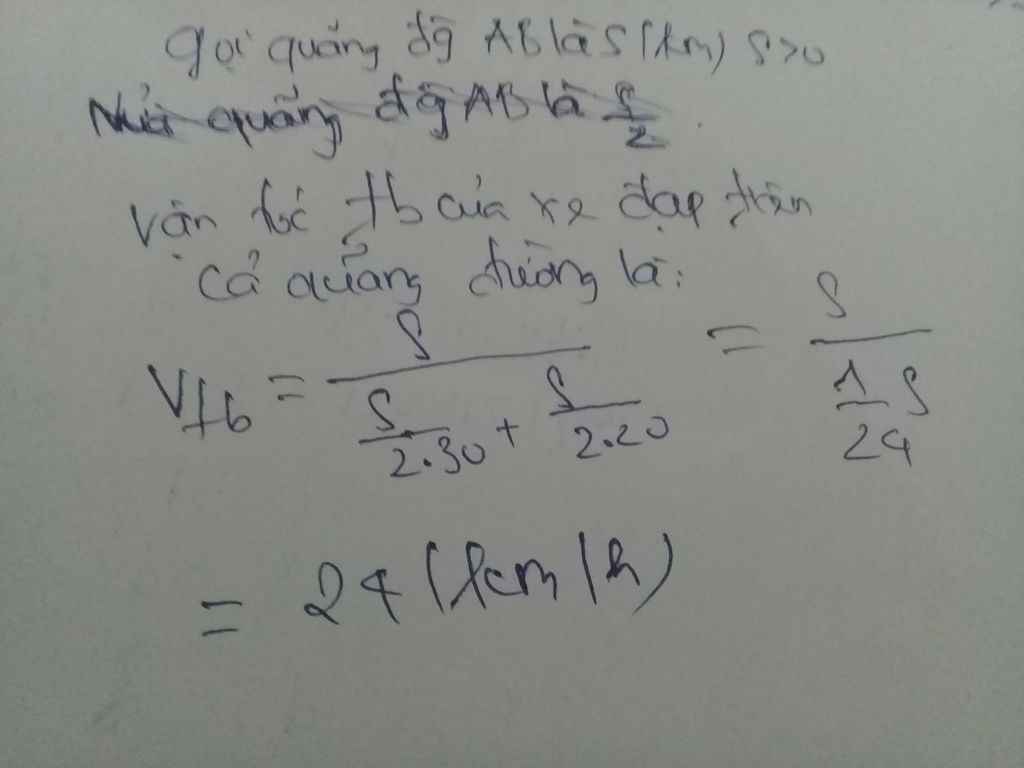

Giải:
Vận tốc trung bình trên cả quãng đường là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{\dfrac{s}{2}+\dfrac{s}{2}}{\dfrac{s}{30}+\dfrac{s}{60}}=\dfrac{s}{s\left(\dfrac{1}{30}+\dfrac{1}{60}\right)}=\dfrac{1}{\dfrac{1}{30}+\dfrac{1}{60}}=20\left(km/h\right)\)
Vậy chọn đáp án D