Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc tạo bởi mặt phẳng nghiêng và phương ngang
sin\(\alpha=\dfrac{h}{l}\Rightarrow\alpha=30^0\)
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương song song mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
sin\(\alpha\).P=m.a\(\Rightarrow\)a=5m/s2
thời gian vật đi hết dốc t=\(\sqrt{\dfrac{l}{2a}}\)=2s
b) khi đi hết dốc vận tốc của vật là v=v0+a.t=10m/s2
khi xuống dốc xuất hiện ma sát
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a'}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
-Fms=m.a' (1)
chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-5m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}=2s\)

Giải theo cách dùng định luật bảo toàn nhé.
Chọn mốc thế năng tại chân mặt phẳng nghiêng.
Độ cao của mặt phẳng nghiêng là: \(h=L\sin30^0=5m\)
Lực ma sát tác dụng lên vật: \(F_{ms}=\mu.N=\mu.mg\cos30^0=\dfrac{\sqrt 3}{2}m\)
Cơ năng khi vật ở đỉnh mặt phẳng nghiêng là: \(W_1=m.g.h=50m\)
Cơ năng khi vật ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Công của ma sát là: \(A_{ms}=F_{ms}L=5\sqrt 3 m\)
Độ giảm cơ năng bằng công của lực ma sát
\(\Rightarrow W_1-W_2=A_{ms}\)
\(\Rightarrow 50m-\dfrac{1}{2}mv^2=5\sqrt 3m\)
\(\Rightarrow 50-\dfrac{1}{2}v^2=5\sqrt 3\)
Tìm tiếp để ra v nhé ![]()


Chọn đáp án B
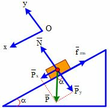
Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động. Vật chịu tác dụng của các lực ![]()
Theo định luật II newton ta có: ![]()
Chiếu Ox ta có
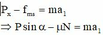
Chiếu Oy ta có:
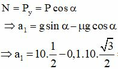
![]()
Vận tốc của vật ở chân dốc. Áp dụng công thức ![]()
![]() m/s
m/s

a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động. Vật chịu tác dụng của các lực f m s → ; N → ; P →
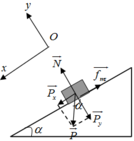
Theo định luật II newton ta có: f → m s + N → + P → = m a → 1
Chiếu Ox ta có :
P x − f m s = m a 1 ⇒ P sin α − μ N = m a 1
Chiếu Oy ta có: N = P y = P cos α
⇒ a 1 = g sin α − μ g cos α
⇒ a 1 = 10. 1 2 − 0 , 1.10. 3 2 = 4 , 134 m / s 2
Vận tốc của vật ở chân dốc.
Áp dụng công thức v 1 2 − v 0 2 = 2 a 1 s
⇒ v 1 = 2 a 1 s = 2.4 , 134.40 ≈ 18 , 6 m / s
b. Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton
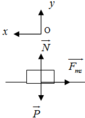
Ta có F → m s + N → + P → = m a → 2
Chiếu lên trục Ox: − F m s = m a 2 ⇒ − μ . N = m a 2 1
Chiếu lên trục Oy: N – P = 0 ⇒ N = P=mg
⇒ a 2 = − μ g = − 0 , 2.10 = − 2 m / s 2
Để vật dừng lại thì v 2 = 0 m / s
Áp dụng công thức:
v 2 2 − v 1 2 = 2 a 2 . s 2 ⇒ s 2 = − 18 , 6 2 2. − 2 = 86 , 5 m

\(\left\{{}\begin{matrix}Ox:mg\sin\alpha-F_{ms}=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha-\mu mg\cos\alpha=ma\)
\(\Rightarrow a=g\sin\alpha-\mu g\cos\alpha=...\left(m/s^2\right)\)
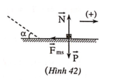
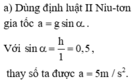

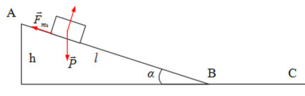

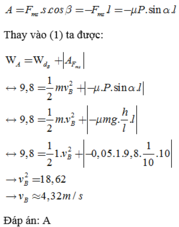
Phân tích lực theo 2 phương Ox: song song với mp nghiêng, chiều dương hướng xuống
Oy: vuông góc với mp nghiêng, chiều dương hướng lên
\(l=h.\sin\alpha=10\sqrt{2}.\dfrac{\sqrt{2}}{2}=10\left(m\right)\)
\(\left\{{}\begin{matrix}Ox:P\cos\alpha-F_{ms}=ma\\Oy:P\sin\alpha=N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mg\cos\alpha-\mu N=m.a\\N=P\sin\alpha\end{matrix}\right.\Leftrightarrow g\cos\alpha-\mu g\sin\alpha=a=...\left(m/s^2\right)\)
b/ \(v^2-v_0^2=2aS\Leftrightarrow v=\sqrt{2.a.l}=...\left(m/s\right)\)
c/ \(t=\dfrac{v-v_0}{a}=\dfrac{v}{a}=...\left(s\right)\)
d/ \(l'=h'\sin\alpha=2\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\left(m\right)\)
\(v'^2=2aS\Rightarrow v=\sqrt{2.a.l'}=...\left(m/s\right)\)