Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Hai động động thành phần có độ lệch pha ∆ φ = ( 2 k + 1 ) π → hai dao động ngược pha => biên độ dao động tổng hợp đạt cực tiểu.

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Đáp án C
Phương pháp : Biên độ dao động tổng hợp của hai dao động cùng phương, cùng tần số, lệch pha π/2:
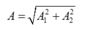
Cách giải:
Do 2 dao động lệch pha góc π/2 => biên độ dao động tổng hợp:
![]()

Biên độ dao động tổng hợp thỏa mãn: \(\left|A_1-A_2\right|\le A\le\left|A_1+A_2\right|\)
\(\Rightarrow\) A = 5 (cm) thỏa mãn hệ thức

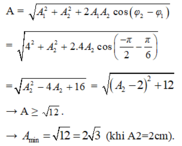
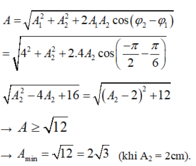
Chọn D
+ Ta thấy: A2 = A12 + A22 (102 = 62 + 82)
nên hai dao động thành phần vuông pha với nhau.