Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực kéo về
\(F = -kx= -k.A.\cos (\omega t +\varphi)\)
So sánh với phương trình \(F=-0.8\cos 4t(N)\) => \(\omega = 4\)(rad/s) và \( k.A = 0,8 \)
\(=> m\omega^2 A = 0,8 => A = \frac{0,8}{m\omega^2}= \frac{0,8}{0,5.4^2}= 0,1 m = 10cm.\)

+ Đối chiếu F = − 0 , 96 cos ( 4 t + π / 4 ) ( N ) với biểu thức tổng quát F = - m ω 2 A cos ( ω t + φ ) :
ω = 4 ( r a d / s ) m ω 2 A = 0 , 96 N ⇒ A = 0 , 12 m
Chọn đáp án C

Lực kéo về tác dụng lên vật có độ lớn cực đại là \(F_{max}=kA= m(2\pi f)^2 A = 0,1.4.10.5^2.0,04 = 4N.\)

Đáp án B
Phương pháp: Áp dụng công thức tính lực kéo về
Cách giải:
Tần số góc: ω = 2πf = 10π (rad/s)
Ta có độ lớn lực kéo về F = k x
=> Lực kéo về có độ lớn cực đại :
![]()
=> Chọn B
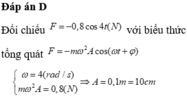

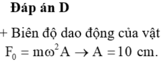
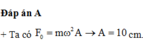
Đáp án D