K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

25 tháng 6 2016
x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
11 tháng 4 2020
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

5 tháng 6 2016
Biên độ: \(A^2=x^2+\dfrac{v^2}{\omega^2}=(2\sqrt 3)^2+\dfrac{(20\sqrt 2)^2}{(10\sqrt 2)^2}\)
\(\Rightarrow A = 4cm\)
\(\cos\varphi = \dfrac{x}{A}=\dfrac{2\sqrt 3}{4}\)
\(v>0\Rightarrow \varphi < 0\)
Suy ra: \(\varphi=-\dfrac{\pi}{6}(rad)\)
Vậy: \(x=4\cos(10\sqrt 2 t-\dfrac{\pi}{6})(cm)\)

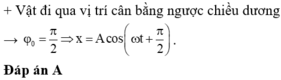
 \
\
f = 20 Hz \(\Rightarrow\) \(\omega\) = 2\(\pi\). f = 2\(\sqrt{10}\). 20 = 40\(\pi\) (rad/s)
x= 2\(\sqrt{3}\) ; A = 4cm
Lúc t=0 (s)
\(\left[\begin{array}{nghiempt}x=2\sqrt{3}\left(1\right)\\v< 0\left(2\right)\end{array}\right.\)
Giải (1) : cosφ = \(\frac{2\sqrt{3}}{4}\)= \(\frac{\sqrt{3}}{2}\)
\(\Rightarrow\) φ = \(\pm\) \(\frac{\pi}{6}\)
Giải (2) : v < 0 \(\Rightarrow\sin\varphi\) >0
Suy ra φ = \(\frac{\pi}{6}\)
PT dao động: \(x=4\cos\left(40\pi t+\frac{\pi}{6}\right)\) (cm)