Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ T = π/10 ⇒ ω = 2π/T = 20 rad/s
+ Trong một chu kì, vật đi được quãng đường là 4A
⇒ 4 A = 40 ⇔ A = 10 c m . v = w A 2 - x 2 = 20 10 2 - 8 2 = 120 c m / s = 1 , 2 m / s

1. Chu kì dao động: T = 4.0,2=0,8s
2. Chu kì T = 2.0,1 = 0,2s
3. \(a=-\omega^2.x\Rightarrow \omega=\sqrt{|\dfrac{a}{x}|}=\sqrt{\dfrac{80}{2}}=2\pi(rad/s)\)
\(\Rightarrow T = 1s\)

Đáp án D
Phương pháp:
- Áp dụng hệ thức độc lập với thời gian của vận tốc và li độ
- Sử dung̣ đường tròn lương̣ giác xác đinḥ pha ban đầu
Cách giải:
Ta có:
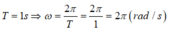
Ta sử dụng phương trình độc lập thời gian để tìm biên độ dao động:
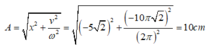
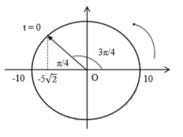
Tai thời điểm ban đầu vật ở vị trí x = - 5 2 và có vận tốc âm. Biểu diễn trên đường tròn lượng giác ta xác định được pha ban đầu của dao động là: φ = 3 π 4 rad
Khi đó ta có phương trình dao động là:
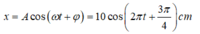

Đáp án C
Phương pháp: Sử dụng lí thuyết về quãng đường đi được của vật dao động điều hoà
Cách giải:
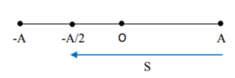
Quãng đường của vật: S = A + A/2 = 1,5A

Đáp án A

+ Biễu diễn các vị trí x = 0 và x = A tương ứng trên đường tròn.
→ Dễ thấy rằng quãng đường mà vật đi được giữa hai vị trí này là: S = 0,5A.

Đáp án B

+ Biễu diễn các vị trí x = – 0,5A và x = A tương ứng trên đường tròn.
→ Dễ thấy rằng quãng đường mà vật đi được giữa hai vị trí này là S = 0,5A + A = 1,5A.

Chọn C
Từ biểu thức tổng quát x = Acos(ωt + φ), ta tìm:
+ A: Quãng đường đi trong 1 chu kỳ là 4A => A = S/4 = 10cm
+ ω: Số dao động trong 1 giây: n = f = N t = 120 60 = 2 ( H z ) => ω = 2πf = 4π rad/s.
+ φ: t = 0 => x = A cosφ = 5; v = -Asinφ < 0 => φ = π/3 rad.
Vậy: x = 10 cos ( 4 πt + π 3 ) cm .

Đáp án A
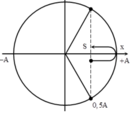
+ Biễu diễn các vị trí x = 0,5A và x = 0,5A theo hai chiều chuyển độngtương ứng trên đường tròn.
→ Dễ thấy rằng quãng đường mà vật đi được giữa hai vị trí này là
S = 0,5A + 0,5A = 1A.
Từ cách biểu diễn trên, ta có thể rút ra được các trường hợp đặc biệt:
Trong khoảng thời gian một chu kì, quãng đường mà vật dao động đi được luôn là 4A.
Trong nửa chu kì quãng đường mà vật nhỏ đi được luôn là 2A
Quãng đường vật đi được trong 1 chu kì là: 4A = 40cm --> A = 10cm.
Chu kì T = 0,5 s --> \(\omega=2\pi/T=4\pi(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow v = \pm\omega\sqrt{A^2-x^2}=...\)