Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Từ đáp án của bài ra suy ra a và b khác nhau.
Từ giả thiết: Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng bằng a với khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng bằng b ta có phương trình: (Lấy trường hợp đại diện)
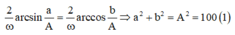
Mặt khác vị trí mà vật có tốc độ 2 π ( b - a ) thỏa mãn
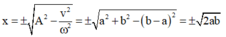
Khi đó khoảng thời gian mà tốc độ của vật không vượt quá 2 π ( b - a ) trong một chu kỳ là
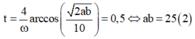
Từ (1) và (2) ta có phương trình
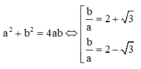
Từ đó ta có
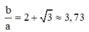

Chọn B
+ Áp dụng định luật bảo toàn năng lượng:
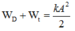
+ Động năng bằng nửa cơ năng =>
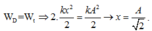
+ Trên vòng tròn lượng giác thấy cứ sau t = T/4 thì động năng lại bằng nửa cơ năng
=> T/4 = π/40 => T = π/10 (s).
+ Tại t = 0: ![]() => thời điểm đầu tiên vận tốc bằng 0 là
=> thời điểm đầu tiên vận tốc bằng 0 là 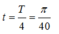
Và cứ sau đó T/2 thì vận tốc lại bằng 0 => Tại những thời điểm vật có vận tốc bằng không là 

Tham khảo:
Trong 1 chu kì thì động năng bằng 4 lần thế năng.
Vị trí động năng bằng thế năng là: \(x=\dfrac{A\sqrt{2}}{2}\) ứng với góc quét \(\dfrac{\pi}{4}\)
Mà: \(2018=2016+2\)
Kể từ thời điểm \(t=0\) ứng với 2016 lần quay \(t=0\) là: \(t_1=504T\)
Hai lần tiếp theo vật đi từ \(t=0\) đến vị trí A trong vòng tròn lượng giác tương ứng với thời gian là:
\(t_2=\dfrac{T}{4}+\dfrac{T}{8}=\dfrac{2T}{8}+\dfrac{T}{8}=\dfrac{3T}{8}\)
Vậy thời điểm động năng bằng thế năng lần thứ 2018 là:
\(t=t_1+t_2=504T+\dfrac{3T}{8}=\dfrac{4035T}{8}\)
\(t=\dfrac{4035}{8}\cdot\dfrac{2\pi}{10\pi}=100,875\left(s\right)\)

Chọn B
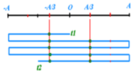
+ Khi Wđ = 8Wt => x = ±A/3 = ±4/3 cm và T = 2s.
+ t1 = 1/6s => x1 = 0cm; t2 = 13/3 s => x2 = -2cm.
![]()
+ Ta thấy cứ 1T vật đi qua 2 vị trí x = ±4/3 cm tất cả 4 lần.
=> Sau 2T vật đi qua 8 lần.
Khi đó, vật ở vị trí x1 = 0cm (VTCB) đi tiếp lượng T/12 đến x2 = -2cm qua vị trí x = -4/3 cm một lần nữa. Ta có hình ảnh minh họa hình trên.
=> Tổng cộng vật đi qua vị trí động năng bằng 8 lần thế năng 9 lần.

-khoảng thời gian 2 lần liên tiếp qua vị trí cân bằng là o,5s có nghĩa là trong 0,5 s đó vật đi dc 2A ( vì ta biết là vật dao động từ VTCB đến điểm biên rùi trở lại VTCB .đoạn đó =2A nhá)
- Ta bjk 1 chu kì là 4A vậy 2A là 1/2 chu kì, mà tg đi 2A = 0,5s vậy 4A =1s, suy ra T=1s,..
- Quãng đường vật đi dc trong 2s là 32cm, vì T=1s nên 2s là 2T mà 2s đi dc 32 cm, nên 8A=32 ( vì T=4A chắc ai cũng bjk  ) => A =4cm ..
) => A =4cm ..
- T=1 => ω =2 tt ( tt nghĩa là số pi nhá).
- bi giờ đi tìm pha ban đầu (ψ )
ta có pt : x = Acos(ωt + ψ)
-tại t=1,5 thì x= 2√3 thế vô ta dc:
2√3=4cos(2 tt * 1,5 + ψ)
=> ψ = - tt/6
Vậy PT là : x= 4cos(2 tt * t - tt/6)..|-)

Chọn A
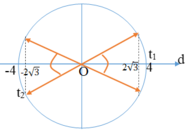
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

Đáp án A
Khoảng thời gian giữa hai lần liên tiếp qua VTCB 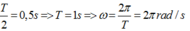
Phương trình dao động của vật có dạng ![]()
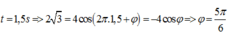

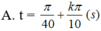
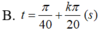


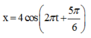
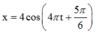
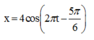
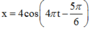
\(A=4\) cm; \(T=\frac{2\pi}{\omega}=2\left(s\right)\)
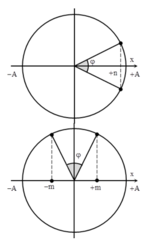
Góc quét của vecto trên đường tròn:
\(\alpha=2.arcsin\frac{2\sqrt{2}}{4}=2.45^0=90^0\)
\(\Rightarrow\) Vecto quét được \(\frac{1}{4}\) đường tròn \(\Rightarrow t=\frac{T}{4}=\frac{1}{2}\left(s\right)\)