
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

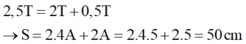

30 10 -10 M N
Vật cách VTCB không quá 10cm, suy ra:|x|<10cm
Vị trí đó được biểu diễn như véc tơ quay trên hình vẽ.
1/3 chu kỳ, véc tơ quay 1/3 * 360 = 1200
Như vậy, mỗi góc nhỏ là 300 như hình vẽ, suy ra biên độ là 2.10 = 20cm
Quãng đường vật đi đc lớn nhất khi nó đi quanh VTCB. Trong thời gian 1/6 chu kỳ, góc quay là 1/6 * 360 = 600
Như vậy, ứng với véc tơ quay từ M đến N.
Quãng đường Max = 10 + 10 = 20cm.

Biên độ dao động: A = 5cm.
Quãng đường vật đi trong một chu kì: 4A = 4.5 = 20cm.

Phương trình tổng quát: \(x = A\cos(\omega t +\varphi)\)
+ Quãng đường khi vật thực hiện 5 dao động: S = 5.4A = 100 cm \(\Rightarrow\) A = 5cm.
+ Tần số: f = 5/2 = 2,5 Hz \(\Rightarrow \omega = 2\pi f = 2\pi.2,5 = 5\pi \ (rad/s)\)
+ t= 0 khi vật có x0=5 nên vật đang ở biên độ dương \(\Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x=5\cos(5\pi t) \ (cm)\)

Tốc độ trung bình \(v = \frac{\text{quãng đường đi được}}{t} \)
Vời thời gian t = 1,6s là không đối tức là \(v_{min} <=> S_{min}\)
Ta có: \(T = \frac{60s}{50} = 1,2s ; A = \frac{16}{2} = 8cm.\)
Nhận xét \(t = 1,6 > T/2 = 0.6 \) nên ta tách: \(t = 2.0,6+0.4 = 2.t_1+t_2\)
Ta sẽ đi tìm quãng đường nhỏ nhất ứng với thời gian \(t_1 = 0.6 s\). Để tìm được quãng đường nhỏ nhất ứng với \(t_1 = 0.6 s\) ta sẽ dùng đường tròn và quỹ đạo của vật sẽ lấy vị trí biên làm trung điểm. Tức là
Góc quay đương ưng với \(t_1 = 0.6 s\) là \(\varphi _1 = t_1 \omega = 0.6\frac{2\pi}{1,2} = \pi.\) Cung quay được sẽ lấy biên làm trung điểm tức là cung \(\stackrel\frown{MaN} = \pi\)
π/2 π/2 A M a N
=> \(S_{1min} = 2. A. (1)\) (2 lần đoạn màu đỏ trên hình ứng với đi từ N đến biên A rồi từ biên A đến điểm M)
Chú ý là quãng đường đường đi được trong t = T/2 thì luôn luôn là 2A. Nên có thể không cần tính mà áp dụng luôn.
Tương tự ta sẽ tìm quãng đường nhỏ nhất ứng với thời gian \(t_2 = 0.4 s\) => \(\varphi _2 = t_2 \omega = 0.4\frac{2\pi}{1,2} = \frac{2\pi}{3}.\)
A 2 A a π/3 π/3 P Q
=> \(S_{2min} = 2. (A - \frac{A}{2} ). (2)\) (2 lần đoạn màu đỏ trên hình ứng với đi từ Q đến biên A rồi từ biên A đến điểm P)
Từ (1) và (2) ta thu được \(v_{min} = \frac{S_{min}}{t} = \frac{2S_{1}+S_2}{t} = \frac{4A+2(A-\frac{A}{2})}{1,6} = \frac{A. (6-1)}{1,6} =25 cm/s.\)
Như vậy đáp án thu được là D. 25cm/s.

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ \(\omega = \frac{2\pi}{T} = \frac{2\pi}{2} = \pi\) (rad/s)
+ Nhận xét: Trong 2s = 1T, vật đi quãng đường 4.A = 40 cm, \(\Rightarrow\) A=10cm.
+ t = 0, vật qua VTCB theo chiều dương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ \\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình: \(x = 10cos(\pi t -\frac{\pi}{2})\) (cm)

Đáp án B
Trong 1T vật đi được quãng đường S = 4A = 20 cm
® Trong 2,5T vật đi được quãng đường S’ = 10A = 50 cm.

Áp dụng: \(v_{max} = \omega A \Rightarrow A = \frac{v_{max}}{\omega} = 120/20 =6 \ cm\)
Li độ trễ pha \(\frac {\pi}{2}\) so với vận tốc, nên ta có phương trình dao động là: \(x = 6\cos(10 t - \frac{\pi}{2}) \ (cm)\)
Thay t = T/6 vào phương trình trên, ta được x = \(3\sqrt3 \ cm\)

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)