Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Khi qua VTCB vật đạt vận tốc cực đại: \(v_{max}=\omega.A=62,8(cm/s)=20\pi(cm/s)\)
+ Khi vật ở biên thì gia tốc cực đại: \(a_{max}=\omega^2.A=200cm/s^2\)
Giải hệ pt trên ta tìm đc \(\omega=\pi(rad/s) \); \(A=20cm\)

Áp dụng: \(v_{max} = \omega A \Rightarrow A = \frac{v_{max}}{\omega} = 120/20 =6 \ cm\)
Li độ trễ pha \(\frac {\pi}{2}\) so với vận tốc, nên ta có phương trình dao động là: \(x = 6\cos(10 t - \frac{\pi}{2}) \ (cm)\)
Thay t = T/6 vào phương trình trên, ta được x = \(3\sqrt3 \ cm\)

1. Chu kì dao động: T = 4.0,2=0,8s
2. Chu kì T = 2.0,1 = 0,2s
3. \(a=-\omega^2.x\Rightarrow \omega=\sqrt{|\dfrac{a}{x}|}=\sqrt{\dfrac{80}{2}}=2\pi(rad/s)\)
\(\Rightarrow T = 1s\)

Chú ý là vận tốc trung bình khác với tốc độ trung bình
Vận tốc trung bình trong một chu kì bằng 0.
Tốc độ trung bình = Quãng đường đi được/ thời gian đi
=> \(v_{tb} = \frac{S}{t} \)
Quãng đường đi được trong một chu kì là \(S = 4A.\)
=> \(v_{tb} = \frac{S}{t} = \frac{4A}{T} =\frac{4.A.\omega}{2\pi} = \frac{4v_{max}}{2\pi} = \frac{4.31,4.10^{-2}}{2.3,14} = 0,2 m/s.\)
Chọn đáp án.A
Vtb=\(\dfrac{2V_{max}}{\pi}\) =\(\dfrac{2.31,4}{3,14}\)=20cm/s

Nửa chu kỳ vật đi được quãng đường S=2A=10\(\Rightarrow A=5\left(cm\right)\)
Dùng công thức độc lập:
\(A^2=x^2+\frac{v^2}{\omega^2}\Leftrightarrow5^2=3^2+\frac{\left(16\pi\right)^2}{\omega^2}\Rightarrow\omega=4\pi\\ \Rightarrow T=\frac{1}{2}\left(s\right)\)
S=10 =>A=5
A2=x2 +v2/ω2 =>ω2=v2/(A2-x2) =>ω=4π
=>T=2π/ω=2π/4π=1/2=0,5s

Phương trình tổng quát: x = \(A\cos(\omega t+\varphi)\)
+ Tần số: f= 120/60 = 2 Hz \(\Rightarrow \omega = 2\pi f = 2\pi .2 = 4\pi\) (rad/s)
+ Biên độ: A = 40/4 = 10 (cm) (1 chu kì vật đi quãng đường là 4A)
t=0, vật có li độ dương, chiều hướng về VTCB, nên v0<0.
\(\Rightarrow\left\{ \begin{array}{} x_0 = 5\ cm\\ v_0 <0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 5/10=0,5\ \\ \sin \varphi > 0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\)
Vậy phương trình: \(x=10\cos(4\pi t +\frac{\pi}{3})\)

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
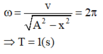
+ Biên độ dao động: A = 40/2 = 10 cm.
+ Áp dụng: \(A^2 = x^2 +\frac{v^2}{\omega^2} \Rightarrow \omega = \sqrt{\frac{v^2}{A^2-x^2}} \Rightarrow \omega = 2\pi \Rightarrow T =1 \ s\)
cho mk hoi sao lai 40/2 lai = 10