Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính quãng đường đi được, ta sử dụng công thức sau:
Quãng đường đi được = |x(t2) - x(t1)|
Với t2 = 13/6 s và t1 = 0, ta có:
x(t2) = 10cos(2π(13/6) - π/3) cm x(t1) = 10cos(2π(0) - π/3) cm
Thay vào công thức, ta tính được quãng đường đi được.
Với phương trình x = 20cos(10πt + π/6) cm, ta cần tính thời điểm vật đi qua vị trí M có li độ 10 cm lần thứ 2023.Để tính thời điểm vật đi qua vị trí M, ta sử dụng công thức sau:
t = (1/10π)arccos((x - 10)/20) - π/6
Thay vào công thức, ta tính được thời điểm vật đi qua vị trí M lần thứ 2023.
Vậy, ta đã giải được bài toán.

Biểu thức động năng biến thiên theo thời gian:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\omega^2A^2sin^2\left(\omega t+\varphi\right)\)
\(\Rightarrow W_đ=\dfrac{1}{2}\cdot0,5\cdot0,1^2\cdot sin^2\left(\pi t+\dfrac{\pi}{3}\right)=0,0025sin^2\left(\pi t+\dfrac{\pi}{3}\right)\left(J\right)\)
Biểu thức thế năng biến thiên theo thời gian:
\(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}kA^2cos^2\left(\omega t+\varphi\right)\)
\(\Rightarrow W_t=\dfrac{1}{2}\cdot m\omega^2A^2cos^2\left(\omega t+\varphi\right)=0,025cos^2\left(\pi t+\dfrac{\pi}{3}\right)\left(J\right)\)

2:
\(x=-3\cdot cos\left(2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(pi+2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(2pi\cdot t+2pi\right)\)
Biên độ là A=3
Tần số góc là 2pi
Chu kì là T=2pi/2pi=1
Pha ban đầu là 2pi
Pha của dao động tại thời điểm t=0,5 giây là;
\(2pi\cdot0.5+2pi=3pi\)
bài 1:
Biên độ góc: A = 5 cm
Tần số góc = 10 pi
Chu kì T = 2pi / tần số góc = 0,2 s
pha dao động là 10 pi x 1 - pi /2 = 19/ 2 pi

\(\omega=20\left(\dfrac{rad}{s}\right)\)
\(A^2=x^2+\dfrac{v^2}{\omega}\)
\(\Rightarrow A=\sqrt{\left(-4\right)^2+\dfrac{\left(-80\right)^2}{20^2}}=4\sqrt{2}\)
\(cos\varphi=\dfrac{4}{4\sqrt{2}}=\dfrac{1}{\sqrt{2}}\Rightarrow\varphi=\dfrac{\pi}{4}\)
Phương trình dao động:
\(x=4\sqrt{2}cos\left(20t+\dfrac{\pi}{4}\right)\)

Với t = 0s, ta được: \(x=8sin\left(2\pi\cdot0-\dfrac{\pi}{3}\right)=-4\sqrt{3}\left(cm\right)\)
Vật đang chuyển động theo chiều dương từ VTCB đến biên dương.
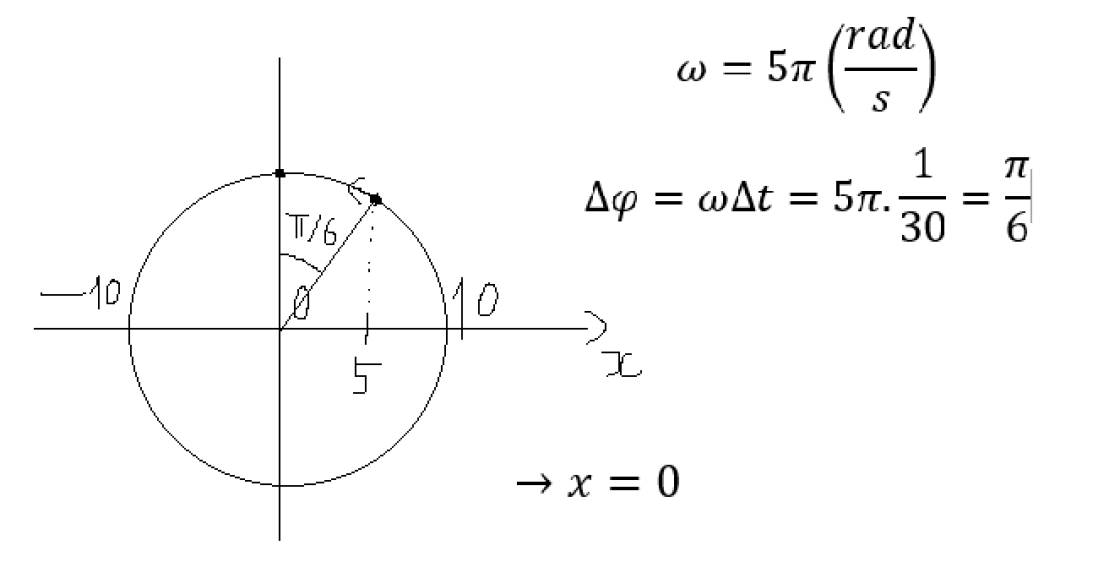
\(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\pi}=2\left(s\right)\)
Trong 1 nửa chu kì, vật di chuyển được quãng đường là \(2\cdot10=20\left(cm\right)\)
Vật khi đó phải đi từ vị trí có pha bằng \(-\dfrac{\pi}{3}\) đến vị trí có pha bằng \(\dfrac{\pi}{3}\), vì vật sẽ di chuyển được quãng đường \(\dfrac{A}{2}+\dfrac{A}{2}=A=10\left(cm\right)\)
Vậy thời gian vật phải đi là: \(\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{2}{2}+\dfrac{2}{6}=\dfrac{4}{3}\left(s\right)\)