Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

\(Acos\left(\omega t=\varphi\right)\)
\(v=-A\omega sin\left(\omega t+\varphi\right)\)
\(a=-A\omega^2cos\left(\omega t+\varphi\right)\)
t = 0
\(x=Acos\varphi=-\sqrt{2}\)
\(v=-A\omega sin\varphi=-\pi\sqrt{2}\)
\(a=-A\omega^2cos\varphi=\pi^2\sqrt{2}\)
Lấy a chia cho x ta được \(\omega=\frac{\pi rad}{s}\)
v chia cho a ta được \(tan\varphi=-1\) mà cos góc này nhỏ hơn 0 nên \(\varphi=\frac{3\pi}{4}\)
A=2cm
Vậy \(x=2cos\left(\pi t+\frac{3\pi}{4}\right)cm\)

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Đáp án B
Giả sử x = Acos ( ωt + φ )
Thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là nửa chu kỳ nên
![]()
Quãng đường đi được trong 2s (2 chu kì) là: S=2.4A=32 =>A=4cm
Tại thời điểm t=1,5s vật qua vị trí có li độ 2 3 cm theo chiều dương
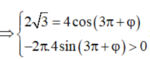
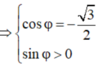
Suy ra, có thể lấy φ = - 7 π 6

Chọn đápán B.
Giả sử x = A cos ω t + φ
Thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là nửa chu kỳ nên
T = 2.0 , 5 = 1 s ⇒ ω = 2 π r a d / s
Quãng đường đi được trong 2s (2 chu kì) là: S = 2.4 A = 32 ⇒ A = 4 c m
Tại thời điểm t = 1 , 5 s vật qua vị trí có li độ x = 2 3 cm theo chiều dương
⇒ 2 3 = 4 cos 3 π + φ − 2 π .4 sin 3 π + φ > 0 ⇒ cos φ = − 3 2 sin φ > 0
Suy ra, có thể lấy φ = − 7 π 6

Chọn đáp án D
Viết lại phương trình dao động dưới dạng hàm cos: x = A sin ω t = A cos ω t − π 2