Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

\(\dfrac{2}{3}T=\dfrac{T}{2}+\dfrac{T}{6}\)
+ Trong thời gian T/2 quãng đường vật đi được luôn là 2A (không có min, max)
+ Như vậy, ta cần tìm quãng đường nhỏ nhất trong thời gian T/6.
Biểu diễn dao động bằng véc tơ quay, trong thời gian T/6 thì véc tơ quay được góc là: 360/6 = 600.
Quãng đường nhỏ nhất khi vật đi tốc độ bé nhất --> Vật đi quanh vị trí biên.
\(\Rightarrow S_{min}=2.(A-A\cos 30^0)=2A(1-\cos 30^0)\)
Tổng quãng đường nhỏ nhất là: \(2A+2A(1-\cos 30^0)=2A(2-\cos 30^0)==2.4.(2-\cos 30^0)=9,07cm\)
Chọn đáp án C.

Vật qua x = 2cm là qua M1 và M2
Vật quay 1 vòng (1 chu kì) qua x = 2 là 2 lần.
Qua lần thứ 2009 thì quay 1004 vòng rồi đi từ M0 đến M1
Từ hình vẽ ta có góc quét :
\(\Delta\varphi=1004.2\pi+\frac{\pi}{6}\Rightarrow t=\frac{\Delta\varphi}{\omega}=502+\frac{1}{24}=\frac{12049}{24}s\)

Ta có: \(F=-k.x\)
\(\Rightarrow x = -\dfrac{F}{k}=-0,05\cos(2\pi t-\dfrac{5\pi}{6})(m)\)
Vận tốc: \(v=v'_{(t)}=0,1.\pi.\sin(2\pi t-\dfrac{5\pi}{6})\)(m/s)
Đến đây chưa xong nha
Bạn phải biến đổi tiếp từ x = -0,05.cos(2πt - \(\dfrac{5\pi}{6}\)) = 0,05.cos(2πt - \(\dfrac{\pi}{6}\))(m)
=> x = 5.cos(2πt - \(\dfrac{\pi}{6}\)) (cm)
=> v = 10π.sin(2πt - \(\dfrac{\pi}{6}\)) = 10π.cos(2πt + \(\dfrac{2\pi}{3}\)) < Đây mới là đáp án cuối cùng nha>
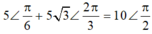



Đáp án D
Phương pháp: Sử dụng lí thuyết về dao động điều hoà
Pha dao động: (2πt + π/3)