Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C 30 0
Chọn mốc thế năng tại chân mặt phẳng nghiêng.
a) Cơ năng tại đỉnh mặt phẳng nghiêng
\(W=mgh=mg.AB\sin 30^0=1,2.10.AB.\sin 30^0=24\)
\(\Rightarrow AB = 4(m)\)
b) Tại D động năng bằng 3 lần thế năng, ta có: \(W_đ=3W_t\Rightarrow W = 4W_t \Rightarrow W_t = 24: 4 = 6(J)\)
\(\Rightarrow mgh_1=mg.DB\sin 30^0=1,2.10.DB.\sin 30^0=6\)
\(\Rightarrow DB = 1(m)\)
c) Tại trung điểm mặt phẳng nghiêng
Thế năng: \(W_t = mgh_2=mg.\dfrac{AB}{2}\sin 30^0=1,2.10.2.\sin 30^0=12(J)\)
Động năng: \(W_đ=W-W_t=24-12=12(J)\)
\(\Rightarrow \dfrac{1}{2}.1,2.v^2=12\)
\(\Rightarrow 2\sqrt 5(m/s)\)
d) Công của lực ma sát trên mặt ngang: \(A_{ms}=\mu mg.S\)
Theo định lí động năng: \(W_{đ2}-W_{đ1}=-A_{ms}\Rightarrow 0-24=-\mu.1,2.10.1\Rightarrow \mu = 2\)
anh ơi , anh quên tính vận tốc của vật tại chân mặt phẳng nghiêng kìa . Đãng trí quá .
a. Áp dụng định lý động năng
A = W d B − W d A ⇒ A F → + A f → m s = 1 2 m v B 2 − 1 2 m v A 2
Công của lực kéo A F = F . s = 4000.100 = 4.10 5 ( J )
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m . g . s = − μ .2000.10.100 = − μ .2.10 6 ( J ) ⇒ 4.10 5 − μ .2.10 6 = 1 2 .2000.20 2 − 1 2 .2000.10 2 ⇒ μ = 0 , 05
b. Giả sử D làvị trí mà vật có vận tốc bằng không
Áp dụng định lý động năng
A = W d D − W d B ⇒ A P → + A f → m s = 1 2 m v D 2 − 1 2 m v B 2
Công trọng lực của vật
A P → = − P x . B D = − m g sin 30 0 . B D = − 10 4 . B D ( J )
Công của lực ma sát
A f m s = − f m s . B D = − μ N . B D = − μ . m . g cos 30 0 . B D = − 2000. B D ( J )
⇒ − 10 4 . B D − 2000. B D = 1 2 .2000.0 − 1 2 .2000.20 2 ⇒ B D = 33 , 333 ( m )
⇒ B C > B D nên xe không lên được đỉnh dốc.
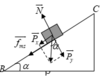
c. Áp dụng định lý động năng
A = W d C − W d B ⇒ A F → + A P → + A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công trọng lực của vật
A P → = − P x . B C = − m g sin 30 0 . B C = − 10 4 .40 = − 4.10 5 ( J )
Công của lực ma sát
A f m s = − f m s . B C = − μ N . B C = − μ . m . g cos 30 0 . B C = − 2000.40 = − 8.10 4 ( J )
Công của lực kéo
A F → = F . B C = F .40 ( J ) ⇒ F .40 − 4.10 5 − 8.10 4 = 0 − 1 2 .2000.20 2 ⇒ F = 2000 ( N )
a) Bảo toàn năng lượng: \(mgh=\dfrac{1}{2}mv^2\Rightarrow v=...\)
b) Khi động năng bằng thế năng thì thế năng bằng một nửa cơ năng:\(mgh'=\dfrac{1}{2}mgh\Rightarrow h'=...\)
c) Dùng biến thiên động năng: \(0-\dfrac{1}{2}mv^2=\mu mg.s\Rightarrow s=...\)
chúc Tết.
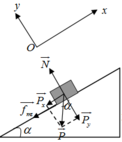
a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
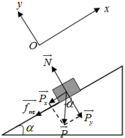
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a →
Chiếu Ox ta có − P x − f m s = m a
⇒ − P sin α − μ N = m a ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1) ⇒ − P sin α − μ P cos α = m a
⇒ a = − g sin α − μ g cos α
Mà sin α = 30 50 = 3 5 ; cos α = 50 2 − 30 2 50 = 4 5
⇒ a = − 10. 3 5 − 0 , 25.10. 4 5 = − 8 m / s 2
Khi lên tới đỉnh dốc thì v = 0 m / s ta có
v 2 − v 0 2 = 2 a s ⇒ 0 2 − v 0 2 = 2. − 8 .50 ⇒ v 0 = 20 2 m / s
b. Khi lên đỉnh dốc thì vật tụt dốc ta có: Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
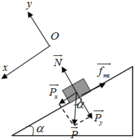
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a → 1
Chiếu Ox ta có: P x − f m s = m a 1
⇒ P sin α − μ N = m a 1 ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1)
⇒ P sin α − μ P cos α = m a 1 ⇒ a 1 = g sin α − μ g cos α
⇒ a 1 = 10. 3 5 − 0 , 25.10. 4 5 = 4 m / s 2
Áp dụng công thức
v 2 2 − v 2 = 2 a 1 s ⇒ v 2 = 2. a 1 . s = 2.4.0 , 5 = 2 m / s
Thời gian vật lên dốc
v = v 0 + a t 1 ⇒ t 1 = − v 0 a = − 20 2 − 8 = 5 2 2 s
Thời gian xuống dốc
v 2 = v + a 1 t 2 ⇒ t 2 = v 2 a 1 = 2 4 = 0 , 5 s
Thời gian chuyển động kể từ khi bắt đầu lên dốc cho đến khi xuống đến chân dốc : t = t 1 + t 2 = 5 2 2 + 0 , 5 = 4 , 04 s
a. Vì Xe chuyển động thẳng đều nên
F = f m s = μ N = μ m g = 0 , 2.2000.10 = 4000 ( N )
b. v C = 72 ( k m / h ) = 20 ( m / s )
Áp dụng định lý động năng
A = W d C − W d B
Công của trọng lực
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 2000.10. 1 2 . B C = 10 4 . B C ( J )
⇒ 10 4 . B C = 1 2 . m . v C 2 − 1 2 m . v B 2 ⇒ 10 4 . B C = 1 2 .2000.20 2 − 1 2 .2000.2 2 ⇒ B C = 39 , 6 ( m )
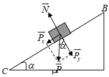
c. Áp dụng định lý động năng
A = W d D − W d C ⇒ A f → m s = 1 2 m v D 2 − 1 2 m v C 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2000.10.200 = − μ .4.10 6 ( J )
Dừng lại
v D = 0 ( m / s ) ⇒ − μ 4.10 6 = 0 − 1 2 .2000.20 2 ⇒ μ = 0 , 1
a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a →
Chiếu Ox ta có − P x − f m s = m a
⇒ − P sin α − μ N = m a ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1) ⇒ − P sin α − μ P cos α = m a
⇒ a = − g sin α − μ g cos α
Mà sin α = 14 50 = 7 25 ; cos α = 50 2 − 14 2 50 = 24 25
⇒ a = − 10. 7 25 − 0 , 25.10. 24 25 = − 5 , 2 m / s 2
b. Khi vật dừng lại thì v = 0 m / s
Gọi s là quãng đường tối đa mà vật đi được cho đến khi dừng lại : ⇒ s = v 2 − v 0 2 2. a = 0 2 − 25 2 2. − 5 , 2 = 60 , 1 m > 50
Vậy vật đi hết dốc. Vận tốc ở đỉnh dốc:
v 1 2 − v 0 2 = 2 a s 1 ⇒ v 1 = 2 a s 1 + v 0 2 = 2. − 5 , 2 .50 + 25 2 = 10 , 25 m / s
v 1 = v 0 + a t 1 ⇒ t 1 = v − v 0 a = 10 , 25 − 25 − 5 , 2 = 2 , 84 s
Câu 2 :
a/\(Wt1−Wt2=m.g.z1−m.g.z2=m.g.(z1+z2)=3.10.(z1+z2)=30(z1+z2)(J)\)mà \(W_{t1}-W_{t2}=500-(-900)=1400(J)\Rightarrow Z=Z_{1}+Z_{2}=\frac{1400}{30}\approx 46,6(m)\)b/Tại vị trí ứng với mức thế năng bằng 0 thì z = 0
thế năng tại vị trí z1 là \(Wt1=m.g.z1⇒z1=5003.10≈16,6(m)\)
vậy vị trí ứng với mức không của thế năng đã chọn cách điểm thả vật 1 khoảng 16,6m
c)ta có
\(v2−v20=2.g.z1⇒v=2.g.z1√=2.10.16,6√=283√(m/s)\)
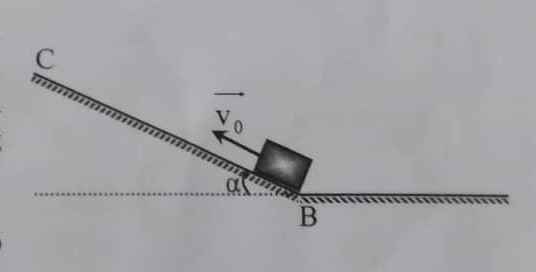
1. Bỏ qua ma sát. Cơ năng đc bảo toàn
a) Chọn mốc thế năng tại mặt đất: Bảo toàn cơ năng: \(\sin\alpha=\dfrac{z_2}{AB}\Rightarrow z_2=\dfrac{4,55}{2}=\dfrac{91}{40}\) (m)
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2=\dfrac{1}{2}mv_2^2+mgz_2\)
\(\Leftrightarrow v_2=\sqrt{v_1^2-2gz_2}=\dfrac{\sqrt{218}}{2}\left(m/s\right)\)
hoặc làm như sau: Dễ chứng minh được: \(a=-g\sin\alpha=-5\left(m/s^2\right)\)
\(v^2-v_0^2=2aS\Rightarrow v=\dfrac{\sqrt{218}}{2}\left(m/s\right)\)
2) Bảo toàn cơ năng ta có:
\(W_1=W_3\Leftrightarrow\dfrac{1}{2}mv_1^2=2mgz_3\Rightarrow z_3=2,5\left(m\right)\)
Gọi khoảng cách từ chân mặt phẳng nghiêng đến nơi có z3=2,5(m) là x ta có:
\(\sin\alpha=\dfrac{z_3}{x}\Rightarrow x=5\left(m\right)\) :D qua điểm B và cách điểm B 0,45 (m)
Tương tự bảo toàn cơ năng part 2: \(W_1=W_3\Leftrightarrow\dfrac{1}{2}mv_1^2=mv_3^2\Rightarrow v_3=\sqrt{\dfrac{1}{2}v_1^2}=5\sqrt{2}\left(m/s\right)\)
b) câu này có nhiều hướng đi nhưng mình xin phép giải theo phương pháp mình dùng nhiều :v
Dễ chứng minh được: \(a=-g\sin\alpha-\mu g\cos\alpha=-6\left(m/s^2\right)\)
\(v_B^2-v_A^2=2aS\Rightarrow v_B=\sqrt{2aS+v_A^2}=\sqrt{\dfrac{227}{5}}\left(m/s\right)\) Vậy vật lên được đến B và vẫn tiếp tục chuyển động