Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chiếu lên phương thẳng đứng
cosα.T1+cosα.T2=P
T1=T2=T
⇒2T.cosα=P⇒T=P2.cosα⇒2T.cosα=P⇒T=P/(2.cosα)
⇒T=15N

chiếu lên phương thẳng đứng
cos\(\alpha.T_1+cos\alpha.T_2=P\)
T1=T2=T
\(\Rightarrow2T.cos\alpha=P\Rightarrow T=\dfrac{P}{2.cos\alpha}\)
\(\Rightarrow T=15N\)

chiếu lên phương thẳng đứng
cosα.T1+cosα.T2=P
T1=T2=T
⇒2T.cosα=P⇒T=P/(2.cosα)
⇒T=15N

chiếu lên phương thẳng đứng
cosα.T1+cosα.T2=P
T1=T2=T
⇒2T.cosα=P⇒T=P/(2.cosα)
⇒T=15N

Hình vẽ và hình biểu diễn lực:
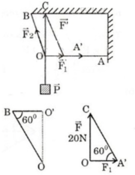
Khi vật cân bằng ta có phương trình lực tác dụng và vật là:
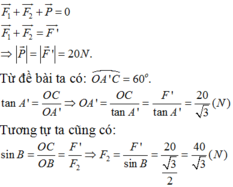

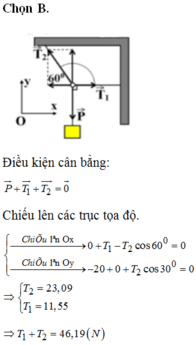
Chọn B.
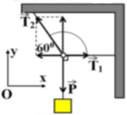
Điều kiện cân bằng: P → + T 1 → + T 2 → = 0 →
Chiếu lên các trục tọa độ.
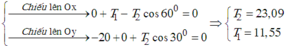
=> T1 + T2 = 46,19 (N)

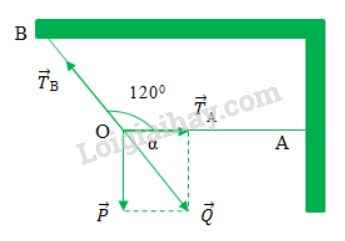
Tham khảo hình vẽ.
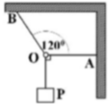
Hệ cân bằng: \(\Leftrightarrow\overrightarrow{P}+\overrightarrow{T_A}+\overrightarrow{T_B}=\overrightarrow{0}\)
Theo quy tắc tỏng hợp lực: \(\overrightarrow{P}+\overrightarrow{T_A}=\overrightarrow{Q}\)
\(\Rightarrow\overrightarrow{Q}+\overrightarrow{T_B}=\overrightarrow{0}\)\(\Rightarrow\left|Q\right|=\left|T_B\right|\)
Có \(\widehat{AOB}=120^o\Rightarrow\alpha=\widehat{T_AOQ}=180^o-120^o=60^o\)
\(P=100N\)
Xét \(\Delta T_AOQ\) vuông tại \(T_A\) có:
\(\left\{{}\begin{matrix}tan\alpha=\dfrac{P}{T_A}\Rightarrow T_A=\dfrac{P}{tan\alpha}=\dfrac{100}{tan60^o}=57,735N\\sin\alpha=\dfrac{P}{Q}\Rightarrow Q=\dfrac{P}{sin\alpha}=\dfrac{100}{sin60^o}=115,47N\end{matrix}\right.\)

Chọn A.
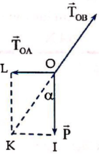
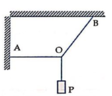
Các lực tác dụng vào điểm treo O như hình vẽ.
Góc α là góc giữa OP và OB, α = 45°
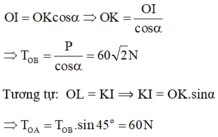
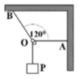
ai đi qua rủ lòng thương giúp em vs ạ
em cần gấp ạ