Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp : Sử dụng công thức tính biên độ dao động tổng hợp và công thức tính cơ năng
Cách giải :
Dễ thấy hai dao động vuông pha nhau nên:
![]()
Thay số ta được:
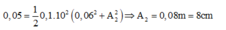

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Chọn C
+ Hai dao động vuông pha: A = A 1 2 + A 2 2 = 8 2 ( c m )
+ Wđ = W – Wt = 1 2 mω2A2 - 1 2 mω2x2 = 1 2 mω2A2 - 1 2 mω2 ( A 2 ) 2
= 3 8 mω2A2 = 3 8 . 0,5.(2π)2. (8 2 .10-2) 2 = 0,096 J = 96mJ.

\(\Delta\varphi=\varphi_2-\varphi_1=\dfrac{\pi}{2}\)
\(A=\sqrt{A_1^2+A_2^2}=6\sqrt{2}\left(cm\right)\)
Phương trình dao động tổng hợp: \(x=6\sqrt{2}cos\left(5\pi t+\dfrac{\pi}{2}\right)cm\)
Cơ năng dao động của vật là:
\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}.0,2.\left(5\sqrt{10}\right)^2.\left(6\sqrt{2}.10^{-2}\right)^2=0,18\left(J\right)=180\left(mJ\right)\)
Chọn A.


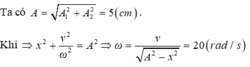
Hướng dẫn: Chọn đáp án A
Biên độ được tính từ công thức:
=> a = 3 cm
=> Chọn A