Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chọn A làm gốc tọa độ, chiều dương A->B, gốc thời gian lúc 7h
1) Phương trình tọa độ của 2 vật:
\(X_1=x_0+vt=6t\)
\(X_2=x_0+v_0t+\frac{1}{2}at^2=400-2t+t^2\)
2) 2 xe gặp nhau : X1=X2
\(\Leftrightarrow6t=400-2t+t^2\)
\(\Leftrightarrow t^2-8t+400=0\)
\(\Delta'=4^2-400< 0\) =>vô nghiệm
Chọn gốc toạ độ là A, chiều dương từ A->B
Xe 1: \(\left\{{}\begin{matrix}v_A=6m/s\\t_{0A}=0\\x_{0A}=0\end{matrix}\right.\)
\(\Rightarrow x_A=v_At=6t\left(m\right)\)
Xe 2: \(\left\{{}\begin{matrix}v_{0B}=-2m/s\\a=-2m/s^2\\t_{0B}=0\\x_{0B}=400m\end{matrix}\right.\)
\(\Rightarrow x_B=x_{0B}+v_{0B}t+\frac{1}{2}at^2=400-2t-t^2\)
b/ Để 2 xe gặp nhau<=> xA= xB
\(\Leftrightarrow6t=400-2t-t^2\Leftrightarrow t=16,4\left(s\right)\)
Vậy gặp lúc 7h27' cách A: 6.16,4= 98,4(m)

Gia tốc vật:
\(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot20}{2^2}=10\)m/s2
Quãng đường cách M:
\(v^2-v^2_0=2aS\)
\(\Rightarrow S=\dfrac{v^2-v^2_0}{2a}=\dfrac{12^2-0}{2\cdot10}=7,2m\)

Đáp án B
Hai vật gặp nhau khi chúng đi được quãng đường bằng nhau sau cùng một khoảng thời gian.
Hay ![]()
Vì chuyển độngcủa các vật là chuyển động biến đổi đều nên (1)
![]()
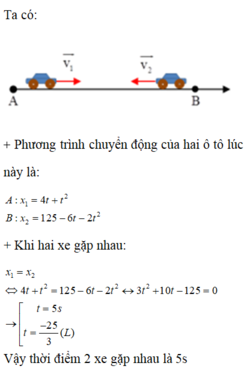
Chú ý: Bài toán có thể giải bằng thiết lập phương trình như sau
Khi hai vật gặp nhau
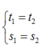
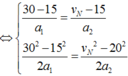
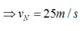
A