Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy trên nửa đường thẳng thẳng kẻ từ A và vuông góc với AB có 4 điểm theo thứ tự M, N, P, Q dao động với biên độ cực đại, nên trên AB có 9 điểm dao động với biên độ cực đai với - 4 ≤ k ≤ 4 ( d2 – d1 = kλ)
A B x M N P Q
Cực đại tại M, N, P, Q ứng với k = 1; 2; 3; 4
Đặt AB = a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB – CA = kλ (*)
CB2 – CA2 = a2 → (CB + CA) (CB – CA) = a2
CB + CA = \(\dfrac{a^2}{k.\lambda}\)(**)
Từ (*) và (**) suy ra \(CA=\dfrac{a^2}{2k.\lambda}-\dfrac{k}{2}\lambda\)
Tại M: ứng với k = 1: MA = \(\dfrac{a^2}{2\lambda}\)- 0,5λ (1)
Tại N: ứng với k = 2: NA = \(\dfrac{a^2}{4\lambda}\)- λ (2)
Tại P: ứng với k = 3: PA = \(\dfrac{a^2}{6\lambda}\) - 1,5 λ (3)
Tại Q: ứng với k = 4: QA = \(\dfrac{a^2}{8\lambda}\) - 2 λ (4)
Lấy (1) – (2) : MN = MA – NA = \(\dfrac{a^2}{4\lambda}\) + 0,5λ = 22,25 cm (5)
Lấy (2) – (3) : NP = NA – PA = \(\dfrac{a^2}{12\lambda}\) + 0,5λ = 8,75 cm (6)
Lấy (5) - (6) → \(\dfrac{a^2}{\lambda}\) = 81 (cm) và λ = 4 cm .
Thế vào (4) → QA = 2,125 cm.
thầy có thể giải thích e chổ CB-CA= Klamda . Với tại s CB= K/2 lamda k thầy?


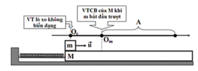
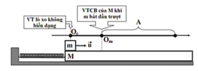
+ Tại t = 0, VTCB O1. Vật dao động A = 4 cm trong 2,5T, tức là vật đi được 10A = 40 cm. Kết thúc quá trình, vật dừng lại ở O2.
+ Tại t = 1s, VTCB O2. Vật đang có vận tốc = 0, li độ = 0 => vật đứng yên trong gđ này.
+ Tại t = 2s, VTCB O3. Vật lại dao động đh A = 4 cm trong 2,5T, đi được 40 cm. Kết thúc quá trình vật đứng yên ở O4.
+ Tại t = 3s, VTCB O4. Vật đứng yên.
+ Tại t = 4s, VTCB O5. Vật dao động A = 4cm, đi được 40 cm và kết thúc dừng lại ở O6.
+ Tại t = 5s, VTCB O6. Vật đứng yên.
Vậy tổng cộng vật đi được 40 x 3 = 120 (cm)

Đáp án A
Vận tốc của hệ hai vật sau khi va chạm
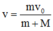
= 0,4 m/s
Quá trình va chạm không làm thay đổi vị trí cân bằng của hệ
→ v = v m a x
→ Biên độ dao động mới
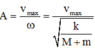
= 5cm

Chọn đáp án A.
+ Ta có: Chu kì dao động của con lắc lò xo nằm ngang:
T = 2 π m k = 0 , 4 s
- Chu kì dao động của con lắc không phụ thuộc vào điện trường.
Gọi O là VTCB đầu tiên khi chưa thiết lập điện trường
- Lần 1 (giây thứ nhất): Khi thiết lập điện trường 1E thì VTCB của CL sẽ là O1, trong đó O chính là 1 vị trí biên và CL dao động xung quanh O1 khi đó:
Fdh1 = F1
=> k. Δ I1 = qE
=> đen ta I1 = TE/k = 4 cm = OO1
* Mặt khác: t = 1s = 2 + 1/2
=> Con lắc ở vị trí biên (giả sử là A1)
=> OA1 = 2OO1
=> Quảng đường:
S1 = 2.4A + 2A = 10A = 10 .OO1 = 10.4 = 40 cm
+ Lần 2 (giây thủ 2): Khi thiết thiết lập điện trường 2E thì vật nặng đang ở vị trí A1 Fdh2 = Fd2
=> k. Δ I2 = q2E
=> Δ I2 = 4.2E / k = 8 cm
- VTCB của CL sẽ là A1, vì con lắc đang đứng yên nên suốt 1s này nó sẽ đứng yên tại vị trí A1
- Tương tự với các giây thứ 3, thứ 4, thứ 5, ta thấy: cứ giây lẻ thì vật đi được 40 cm và giây chẵn thì vật đứng yên
=> Tổng quảng đường vật đi được trong 5s là:
S = S1 + S3 + S5 = 40 + 40 + 40 = 120 cm

uM=Acoss(wt-2pi d/ lamda) = A cos (wt - 2pi/3)
Khi t=T/3 thay vào ta đc: uM = A cos (2pi/3 - 2pi/2) = A = 5
Pt của M: uM = 5 cos (wt - 2pi/3)

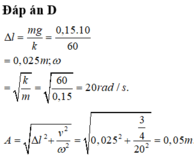
Vì gốc thời gian là lúc quả cầu nhỏ được truyền vận tốc và ban đầu vật được đưa về vị trí lò xo không biến dạng nên ta có tại thời điểm ban đầu x0= -0,025 m và vật đang chuyển động theo chiều dương. Suy ra thời điểm gần nhất vật đi qua vị trí có động năng bằng 3 lần thế năng là lúc x1= 0,025 m; v1=√3/2 m/s.
Vì điện trường đều hướng xuống nên ta có vị trí cân bằng mới của vật bị dịch xuống 1 khoảng:
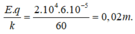

Đáp án C
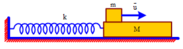
+ Tần số góc của dao động ω = k m = 50 50 . 10 - 3 = 10 π rad s → T = 0 , 2 s .
+ Tại t = 0 kéo vật đến vị trí lò xo giãn 4 cm rồi thả nhẹ → vật dao động với biên độ A 1 = 4 cm quanh vị trí lò xo không biến dạng.
→ Sau khoảng thời gian Δt = 0 , 5 T = 0 , 1 s con lắc đến biên âm (lò xo bị nén 4 cm). Ta thiết lập điện trường, dưới tác động của điện trường vị trí cân bằng của con lắc dịch chuyển ra xa điểm cố định của lò xo, cách vị trí lò xo không biến dạng một đoạn Δl 0 = qE k = 5 . 10 - 6 . 10 5 50 = 1 cm .
→ Biên độ dao động của con lắc sau đó là A 2 = 4 + 1 = 5 cm .
+ Sau khoảng thời gian Δt = 0 , 5 T = 0 , 1 s con lắc đến vị trí biên dương (lò xo giãn 6 cm), điện trường bị mất đi → vị trí cân bằng của con lắc lại trở về vị trí lò xo không biến dạng con → lắc sẽ dao động với biên độ A 3 = 6 cm .
→ v cm s cm s max


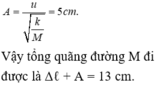


Ta có:
=> Chọn C.