
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

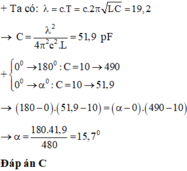

Đáp án A
Coi điện dung của tụ điện là hàm bậc nhất theo góc quay, khi đó: C = kα + C 0
Khi tăng góc quay từ 0 ° đến 180 ° :
C 1 = k . 0 + C 0 = 10 C 2 = k . 180 + C 0 = 490 ⇒ C 0 = 10 k = 8 3 ⇒ C = 8 3 . α + 10 pF
Để bắt được sóng 19,2 m thì điện dung của tụ:
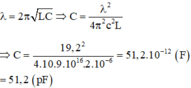
Góc quay của tụ khi đó: C = 8 3 . α + 10 = 51 , 2 ⇒ α = 15 , 45 °
Phải quay các bản tụ một góc α tính từ vị trí điện dung C bé nhất Δα = 15 , 45 − 0 = 15 , 45 °

Đáp án B
Gọi Cx là điện dung của tụ điện ứng giá trị của góc quay α . Ta có:
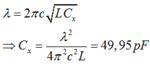
Khi C biến thiên từ C 1 đến C 2 thì góc quay tăng dần từ 0 0 đến 180 0 . Khi C biến thiên từ C 1 đến C x thì góc quay tăng dần từ 0 0 đến α nên:
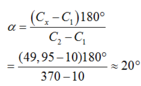

Đáp án C
Khi thay đổi góc xoay của tụ từ 0 ° đến 150 ° thì mạch thu được dải sóng của bước sóng 30 m đến 90 m
90 30 = λ max λ min = C max C min ⇒ C max = 9 C min và C max = C min + 150 − 0 k
Nếu muốn thu được bước sóng 60 m:
2 = 60 30 = λ ' λ min = C ' C min ⇒ C ' = 4 C min
Lại có C ' = C min + C max − C min 150 α nên 4 C min = 8 C min . α 150 + C min ⇒ α = 56 , 25 °

\(\lambda=\frac{v}{f}\) có \(v=\cos st\) đẻ bước song tăng 2 lần thì \(f\) giảm 2 lần có \(f=\frac{1}{2.\pi.\sqrt{LC}}\) suy ra \(C\) tăng 4 lần
để \(C\) tăng phải mắc song song \(C_0=C_1+C_2\)
vậy đáp án là \(3C\)
\(\rightarrow C\)

Ta có : ADCT : \(I_0=U_0\sqrt{\frac{C}{L}}\) ( Từ công thức tính năng lượng điện từ trong mạch \(W=W_{Cmax}=W_{Lmax}\)
Nghĩa là :\(\frac{L.\left(I_0\right)^2}{2}=\frac{C.\left(U_0\right)^2}{2}\))
\(\Rightarrow I_0=5.\sqrt{\frac{8.10^{-9}}{2.10^{-4}}}=\text{0.0316227766}\left(A\right)\)\(\Rightarrow I=\frac{I_0}{\sqrt{2}}=\text{0.022360677977}\left(A\right)\)
Mà \(P=r.I^2\Rightarrow r=\frac{6.10^{-3}}{5.10^{-4}}=12\left(\Omega\right)\Rightarrow D\)