Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Lấy 8 học sinh trong 19 học sinh có C 19 8 = 75582 cách.
Suy ra số phân tử của không gian mẫu là n ( Ω ) = 75582
Gọi X là biến cố “8 học sinh được chọn có đủ 3 khối”
Xét biến cố đối của biến cố X gồm các trường hợp sau:
+ 8 học sinh được chọn từ 2 khối, khi đó có C 14 8 + C 11 8 + C 13 8 cách.
+ 8 học sinh được chọn từ 1 khối, khi đó có C 8 8 cách.
Do đó, số kết quả thuận lợi cho biển cổ X là n ( X ) = C 19 8 - ( C 14 8 + C 11 8 + C 13 8 + C 8 8 ) = 71128 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 71128 75582 .

Gọi A là biến cố : "4 học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình"
Số phần tử không gian mẫu \(\left|\Omega\right|=C^4_{33}=40920\)
Ta có các trường hợp được chọn sau :
(1) Có 2 học sinh giỏi, 1 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^2_{10}.C^1_{11}.C^1_{12}=5940\).
(2)Có 1 học sinh giỏi, 2 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^2_{11}.C^1_{12}=6600\).
(3)Có 1 học sinh giỏi, 1 học sinh khá và 2 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^1_{11}.C^2_{12}=7260\).
Ta được \(\left|\Omega_A\right|=5940+6600+7260=19800\)
Do đó : \(P\left(A\right)=\frac{\left|\Omega_A\right|}{\left|\Omega\right|}=\frac{15}{31}\)

Chọn D
Số cách chọn 6 học sinh từ 15 học sinh là C 15 6 = 5005(cách)
⇒ n ( Ω ) = 5005
Gọi biến cố A: “Chọn được 6 học sinh đủ 3 khối”
=> A ¯ : “Chọn được 6 học sinh không đủ 3 khối”.
Cách 1
+ Trường hợp 1: Chọn 6 học sinh từ 1 khối 1 => Chọn 6 học sinh khối 10 có C 6 6 = 1 (cách).
+ Trường hợp 2: 6 học sinh được chọn trong 2 khối.
* Chọn 6 học sinh trong khối 11 và khối 12 có ![]() (cách).
(cách).
* Chọn 6 học sinh trong khối 10 và khối 12 có ![]() (cách)
(cách)
* Chọn 6 học sinh trong khối 11 và khối 10 có ![]() (cách).
(cách).
Từ 2 trường hợp suy ra ![]()
.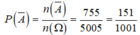
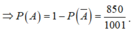 0
0
Cách 2
+ Trường hợp 1: Chọn 6 học sinh từ 1 khối => Chọn 6 học sinh khối 10 có C 6 6 = 1 (cách).
+ Trường hợp 2: 6 học sinh được chọn trong 2 khối có ![]()
Từ 2 trường hợp suy ra ![]()
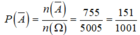
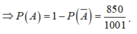

Số cách chọn 8 học sinh gồm hai khối là phần bù của cách chọn 8 học sinh đi dự đại hội sao cho mỗi khối có ít nhất 1 học sinh được chọn.( chú ý mỗi khối đều có ít hơn 8 học sinh).
Số cách chọn 8 học sinh từ hai khối là: ![]() .
.
Số cách chọn 8 học sinh bất kì là: ![]()
Số cách chọn thỏa yêu cầu bài toán: ![]()
Chọn D.

Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có ![]() cách.
cách.
● Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 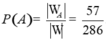
Chọn D.

Đáp án B
Xác suất bằng C 9 2 + C 10 2 + C 3 2 C 22 2 = 4 11 .

Đáp án D
Chọn 4 học sinh bất kỳ có: Ω = C 13 4 = 715
Gọi A là biến cố: “4 học sinh được chọn có đủ 3 khối”
Khi đó
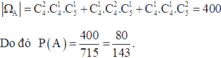
Đáp án D
Phương pháp:
+ ) P ( A ) = n ( A ) n ( Ω )
+ P(A) = 1P( A )
Cách giải: Số phần tử của không gian mẫu: n ( Ω ) = C 18 6
Gọi A: “Mỗi khối có ít nhất 1 học sinh được chọn.”