Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

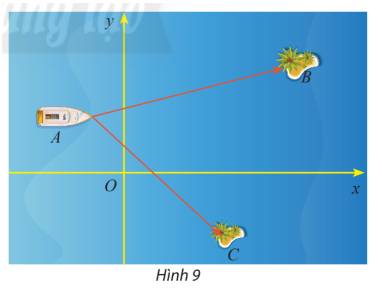
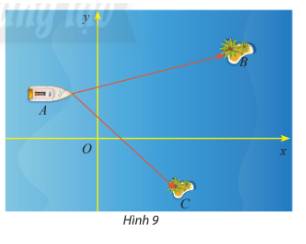
a) Ta có: \(\overrightarrow {AB} = \left( {60;10} \right),\overrightarrow {AC} = \left( {42; - 43} \right),\overrightarrow {BC} = \left( { - 18; - 53} \right)\)
\(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{60.42 + 10.( - 43)}}{{\sqrt {{{60}^2} + {{10}^2}} .\sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} }} \simeq 0,572 \Rightarrow \widehat {BAC} \approx 55^\circ 8'\)
b)
Khoảng cách từ tàu đến đảo B là \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{60}^2} + {{10}^2}} = 10\sqrt {37} \) (km)
Khoảng cách từ tàu đến đảo B là \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} = \sqrt {3613} \) (km)
Dưới đây là đáp án cho các câu hỏi:
a) Tính số đo của góc \(\angle B A C\)
Số đo góc \(\angle B A C \approx 107.48^{\circ}\).
b) Khoảng cách từ con tàu đến hòn đảo B
Khoảng cách từ con tàu đến hòn đảo B là khoảng 72.11 km.
c) Khoảng cách từ con tàu đến hòn đảo C
Khoảng cách từ con tàu đến hòn đảo C là khoảng 45.28 km.

Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà \(AB=d, \hat {B} =\beta; \hat {C} =180^o-\alpha -\beta \)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)

a) Tàu A di chuyển theo hướng vecto \(\overrightarrow {{u_1}} = \left( { - 35;25} \right)\)
Tàu B di chuyển theo hướng vecto \(\overrightarrow {{u_2}} = \left( { - 30; - 40} \right)\)
Gọi \(\alpha \) là góc giữa hai đường đi của hai tàu, ta có:
\(\cos \alpha = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {\left( { - 35} \right).\left( { - 30} \right) + 25.\left( { - 40} \right)} \right|}}{{\sqrt {{{\left( { - 35} \right)}^2} + {{25}^2}} .\sqrt {{{\left( { - 30} \right)}^2} + {{\left( { - 40} \right)}^2}} }} = \frac{1}{{5\sqrt {74} }}.\)
b) Sau t giờ, vị trí của tàu A là điểm M có tọa độ là: \(M\left( {3 - 35t; - 4 + 25t} \right)\)
Sau t giờ, vị trí của tàu B là điểm N có tọa độ là: \(N\left( {4 - 30t;3 - 40t} \right)\)
Do đó, \(\overrightarrow {MN} = \sqrt {{{\left( {1 + 5t} \right)}^2} + {{\left( {7 - 65t} \right)}^2}} = \sqrt {4250{t^2} - 900t + 50} = \sqrt {4250{{\left( {t - \frac{9}{{85}}} \right)}^2} + \frac{{40}}{{17}}} \ge \sqrt {\frac{{40}}{{17}}} \approx 1,53\left( {km} \right)\)
Suy ra MN nhỏ nhất xấp xỉ 1,53km khi \(t = \frac{9}{{85}}\)
Vậy sau \(\frac{9}{{85}}\) giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất và cách nhau 1,53km
c) Vị trí ban đầu của tàu A tại \({M_o}\) ứng với \(t = 0\) , khi đó \({M_o}\left( {3; - 4} \right)\)
Tàu B di chuyển theo đường thẳng có vecto pháp tuyến \(\overrightarrow n = \left( {40; - 30} \right)\) và đi qua điểm \(K\left( {4;3} \right)\) Phương trình tổng quát của là: \(40\left( {x - 4} \right) - 30\left( {y - 3} \right) = 0 \Leftrightarrow 4x - 3y - 7 = 0\) \(\Delta \)
Ta có: \(d\left( {{M_o},\Delta } \right) = \frac{{\left| {4.3 - 3.\left( { - 4} \right) - 7} \right|}}{{\sqrt {{4^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{17}}{5} = 3,4\left( {km} \right)\)
Vậy nếu tàu A đứng yên ở vị trí ban đầu còn tàu B di chuyển thì khoảng cách ngắn nhất giữa hai tàu bằng 3,4km.

Đặt x=B'C(km), 0<=x<=9
=>\(BC=\sqrt{x^2+36};AC=9-x\)
Chi phí xây dựng dường ống là:
\(C\left(x\right)=130000\sqrt{x^2+36}+50000\left(9-x\right)\left(USD\right)\)
Hàm C(x) xác định và liên tục trên [0;9] và \(C'\left(x\right)=10000\left(\dfrac{13x}{\sqrt{x^2+36}}-5\right)\)
C'(x)=0
=>13x=5 căn x^2+36
=>x=5/2

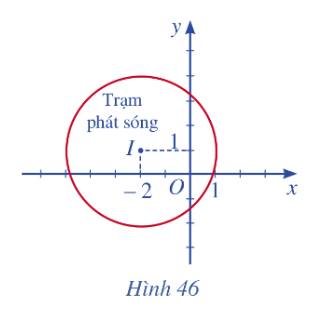
a) Phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
b) Khoảng cách từ tâm I đến A là: \(IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 5 \)
Do \(IA < 3\) nên điểm A nằm trong đường tròn ranh giới. Vậy nên người A có thể dịch vụ của trạm.
c) Khoảng cách từ tâm I đến B là: \(IB = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {10} \)
Khoảng cách ngắn nhất theo đường chim bay để 1 người ở B di chuyển đến vùng phủ sóng là:
\(IB - R = \sqrt {10} - 3\left( {km} \right)\)

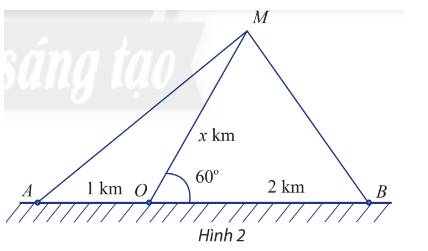
a) Đặt độ dài của MO là x km \(\left( {x > 0} \right)\)
Ta có: \(\widehat {MOA} + \widehat {MOB} = 180^\circ \) (hai góc bù nhau) \( \Rightarrow \widehat {MOA} = 120^\circ \)
Áp dụng định lý Cosin trong tam giác ta tính được:
+) Khoảng cách từ tàu đến B là \(MB = \sqrt {{x^2} + {2^2} - 2.2.x.\cos 60^\circ } = \sqrt {{x^2} - 2x + 4} \)
+) Khoảng cách từ tàu đến A là \(MA = \sqrt {{x^2} + {1^2} - 2.1.x.\cos 120^\circ } = \sqrt {{x^2} + x + 1} \)
b) Theo giải thiết ta có phương trình \(MB = \frac{4}{5}MA \Rightarrow \sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)
\(\begin{array}{l} \Rightarrow {x^2} - 2x + 4 = \frac{{16}}{{25}}\left( {{x^2} + x + 1} \right)\\ \Rightarrow \frac{9}{{25}}{x^2} - \frac{{66}}{{25}}x + \frac{{84}}{{25}} = 0\end{array}\)
\( \Rightarrow x \simeq 1,64\) và \(x \simeq 5,69\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(x \simeq 1,64\) hoặc \(x \simeq 5,69\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Đổi 500 m = 0,5 km
Theo giả thiết ta có phương trình sau:
\(\begin{array}{l}MB = MO - 0,5 \Rightarrow \sqrt {{x^2} - 2x + 4} = x - 0,5\\ \Rightarrow {x^2} - 2x + 4 = {\left( {x - 0,5} \right)^2}\\ \Rightarrow {x^2} - 2x + 4 = {x^2} - x + \frac{1}{4}\\ \Rightarrow x = \frac{{15}}{4}\end{array}\)
Thay \(x = \frac{{15}}{4}\) vào phương trình \(\sqrt {{x^2} - 2x + 4} = x - 0,5\) ta thấy thỏa mãn phương trình
Vậy khi \(x = \frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.

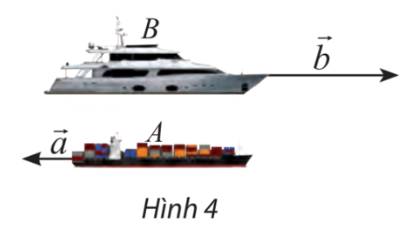
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến