Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài miếng bìa là
\(x\left(cm;x>4\right)\)
Chiều rộng miếng bìa là:
\(\frac{3x}{5}\left(cm\right)\)
Diện tích ban đầu là:
\(\frac{x\times3}{5}=x^2\times\frac{3}{5}\left(cm^2\right)\)
Diện tích mới của miếng bìa là:
\(\left(x-4\right)\times\left(\frac{3x}{5}-1\right)=\frac{1}{2}\times x^2\times\frac{3}{5}\Leftrightarrow x=10\)
Chu vi miếng bìa đó là:
\(2\times\left(10+\frac{3}{5}\times10\right)=32\left(cm\right)\)
Đáp số: 32 (cm)

Gọi chiều dài hcn là a => chiều rộng hcn là a-7
Áp dụng định lí Py-ta-go ta có
\(a^2+\left(a-7\right)^2=13^2\)
\(\Rightarrow a^2+a^2-14a+49=169\)
\(\Rightarrow2a^2-14a=120\)
\(\Rightarrow2a\left(a-7\right)=120\)
\(\Rightarrow a\left(a-7\right)=60\)
Vậy diện tích mảnh vườn là 60 cm2

Gọi chiều dài của tấm bìa là x (x > 3) (dm)
⇒ Chiều rộng của tấm bìa là x – 3 (dm)
Nếu tăng chiều dài 1 dm và giảm chiều rộng 1 dm thì diện tích là 66 d m 2 nên ta có phương trình:
(x + 1)(x – 3 – 1) = 66
⇔ (x + 1)(x – 4 ) = 66
⇔ x 2 – 3x – 4 – 66 = 0
⇔ x 2 – 3x – 70 = 0
Δ = 3 2 - 4.(-70) = 289 ⇒ ∆ = 17
⇒ Phương trình đã cho có 2 nghiệm
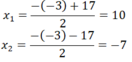
Do x > 3 nên x =10
Vậy chiều dài của tấm bìa là 10 dm
Chiều rộng của tấm bìa là 7 dm.

Gọi chiều dài HCN là x => chiều rộng là x - 3
Khi tăng chiều dài thêm 1/4 của nó tức là: x + 1/4x = 5/4x
Khi tăng chiều rộng thêm 1cm tức là x - 3 + 1 = x - 2
Diện tích ban đầu của HCN là x(x - 3)
Diện tích sau khi thay đổi các kích thước là: 5/4x(x - 2)
Theo đề bài ta có phương trình: x(x - 3) + 20 = 5/4x.(x - 2)
<=> x2 - 3x + 20 = 5/4x2 - 5/2x
<=> 1/4x2 + 1/2x - 20 = 0
<=> x = 8 (n) x = - 10 (l)
=> Chiều dài HCN là 8cm
=> Chiều rộng HCn là 5cm


Gọi chiều dài tờ bìa HCN là x(cm) ( x > 0 )
Khi đó đường chéo tờ bìa là x + 8 (cm)
Theo định lí Py - ta - go, ta có:
\(x^2+24^2=\left(x+8\right)^2\)
\(\Leftrightarrow\)\(x^2+576=x^2+16x+64\)
\(\Leftrightarrow\)\(576-64=16x\)
\(\Leftrightarrow\)\(512=16x\)
\(\Leftrightarrow\)\(x=32\)
Chiều dài tờ bìa HCN là 32cm.
Diện tích tờ bìa là:
32 x 24 = 768 (cm2)