Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Đáp án B.
Gọi S t là quãng đường mà chất điểm đi được sau t giây đầu tiên. Khi đó S t là nguyên hàm của vận tốc v t = t 2 . e − t . Hay S t = ∫ v t d t = ∫ t 2 . e − t d t .
Đặt u = t 2 d v = e − t d t → d u = 2 t d t v = − e − t → S t = − t 2 + e − t + 2 ∫ t . e − t d t
Đặt u 1 = t d v 1 = e − t d t → d u 1 = d t v 1 = − e − t → ∫ t . e − t d t = − t . e − t + ∫ e − t d t = − t . e − t − e − t + C 1
Vậy
S t = − t 2 . e − t + 2 − t . e − t − e − t + C 1 = − e − t t 2 + 2 t + 2 + C

Đáp án C
Ta có: v ' t = 2 t − 2 e t 2 − 2 t = 0 ⇔ t = 1
Hàm số v t = e + e t 2 − 2 t m / s xác định và liên tục trên đoạn 0 ; 10
Ta có: v 0 = e + 1 ; v 1 = e + 1 e ; v 10 = e + e 80
Vậy v min = v 1 = e + 1 e

Đáp án B
Khối bát diện gồm 2 khối chóp tứ giác đều bằng nhau ghép lại.
Ta có: V = 2 V S . A B C D
Ta có: O A = a 2 2 ⇒ S O = S A 2 − O A 2 = a 2 2
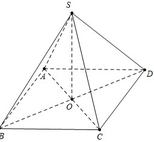
⇒ V S . A B C D = 1 3 S O . S A B C D = 1 3 . a 2 2 . a 2 = a 3 2 6
Do đó V = a 3 2 3 .

Theo đề bài, ta có:
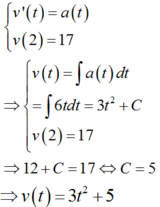
Quãng đường vật đó đi được trong khoảng thời gian tử thời điểm t = 4 giây đến thời điểm t = 10 giây là:
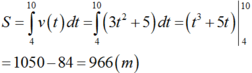
Chọn: D
