Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kỳ 1à khoảng thời gian sóng truyền đi đuợc quãng đuờng bằng 1 buớc sóng
Chọn đáp án B

Ta có: \(\dfrac{\pi x}{4}=\dfrac{2\pi x}{\lambda}\Rightarrow \lambda = 8cm\)
Chu kì: \(T=1s\)
Tốc độ truyền sóng: \(v=\dfrac{\lambda}{T}=8cm/s\)

Bạn tham khảo hai bài tương tự này nhé:
Câu hỏi của Nguyễn Khánh Quỳnh - Học và thi online với HOC24
Câu hỏi của Hue Le - Học và thi online với HOC24

Đáp án A
Phương pháp: Đồng nhất với phương trình sóng dừng và áp dụng công thức tốc độ truyền sóng v = λT
Cách giải:
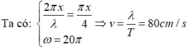

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)


Đáp án B
Phương pháp: Quãng đường sóng truyền đi được trong thời gian t: S = v t
Cách giải:
Đồng nhất với phương trình truyền sóng ta có:
ω = 20 π ( r a d / s ) ⇒ T = 0,1 s 5 π x = 2 π x λ ⇒ λ = 0,4 c m ⇒ v = λ T = 0,4 0,1 = 4 c m / s )
Quãng đường sóng truyền đi được trong 5 giây: S = v t = 4 . 5 = 20 c m