Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
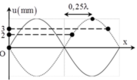
+ Biên độ dao động của một phần tử dây cách nút một gần nhất một khoảng d được xác định bởi biểu thức a = cos 2 π d λ + π 2 hay a = A sin 2 π d λ
+ Hai điểm dao động với biên độ 2 mm gần nhau nhất phải đối xứng qua nút
Hai điểm dao động với biên độ 3 mm gần nhau nhất phải đối xứng qua bụng
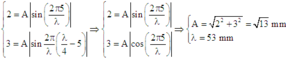
Khoảng cách giữa hai nút sóng liên tiếp là λ 2 = 26 , 7 m m .

Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

Đáp án A
*Hai điểm có cùng biên độ 2mm đối xứng nhau qua nút gần nhất và hai điểm có cùng biên độ 3mm đối xứng nhau qua bụng gần nhất. Do đó ta có:
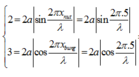
![]()
Giải phương trình ta được: ![]()
Khoảng cách giữa hai nút liên tiếp là ![]()

Áp dụng công thức tính năng lượng điện từ trường ta có
W = Wđ = Wt \(\Rightarrow\frac{1}{2}LI_0^2=\frac{1}{2}lI^2+\frac{1}{2}Cu^2\)
\(\Rightarrow u=\sqrt{\left(I_0^2-I^2\right)\frac{L}{C}}\Rightarrow u=\)\(\sqrt{\frac{0,1}{10^{-5}}\left(0,05^2-0,02^2\right)}=4\left(V\right)\)
chọn A

Biên độ dao động tổng hợp thỏa mãn: \(\left|A_1-A_2\right|\le A\le\left|A_1+A_2\right|\)
\(\Rightarrow\) A = 5 (cm) thỏa mãn hệ thức

\(E=\frac{1}{2}\omega^2A^2\) nên vận tốc truyền sóng không ảnh hưởng.
chọn D

3 vecto của 3 dao động tạo thành tam giác đều (vì cùng biên độ)
Pha ban đầu của dao động thứ 2 là: \(\phi=-\frac{\pi}{12}-\frac{\pi}{3}=-\frac{5\pi}{12}\left(rad\right)\)

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.