

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A
l = k + 1 2 λ 2 = k + 1 2 v 2 ⇒ f = k + 1 2 v 2 l = 2 , 5 ( k + 0 , 5 ) M à 100 ≤ f ≤ 125 ⇒ 39 , 5 ≤ k ≤ 49 , 5

Chọn C
Ta có dây đàn hồi được treo lơ lửng trên một cần rung như vậy ứng với sóng dừng một đầu cố định một đầu tự do
khi đó
l
=
(
2
k
+
1
)
λ
4
=
(
2
k
+
1
)
v
4
f
⇒
f
=
(
2
k
+
1
)
v
4
l
=
2
(
2
k
+
1
)
100 ≤ f ≤ 120 ⇒ 24 , 5 ≤ k ≤ 29 , 5
⇒
Có 5 giá trị k thoả mãn
Như vậy có thể tạo được 5 lần sóng dừng trên dây khi thay đổi tần số rung của cần

Đáp án B
Sóng dừng với một đầu nút, một đầu bụng là
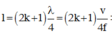
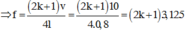
Mà
![]()
Có 5 giá trị tần số cho sóng dừng trên dây.

Chọn B
Do sợi dây treo lơ lửng trên một cần dung, nên đây coi là hiện tượng sóng dừng một đầu cố định, một đầu tự do. Ta có
L
=
(
2
k
-
1
)
λ
4
=
(
2
k
-
1
)
v
1
f
⇔
f
=
(
2
k
-
1
)
v
4
L
. Với các giá trị K = 13,14,15,16,17,18 cho các giá trị của f thỏa mãn f thay đổi từ 80Hz đến 120 Hzvậy có 6 giá trị của tần số có thể tạo sóng dừng

Đáp án D
Để có sóng dừng trên dây thì l = kλ/2.
→ Tần số f = v λ = k v 2 l = 20 k 3 ( H z )
Mà 80 ≤ 20 k 3 ≤ 120 → 12 ≤ k ≤ 18
Có 7 giá trị k nguyên thỏa mãn → có 7 giá trị tần số có thể tạo sóng dừng trên dây.

Em phải post mỗi câu hỏi 1 bài thôi nhé, để tiện thảo luận.
1. Điều kiện có sóng dừng trên dây có một đầu cố định một đầu tự do: \(L=(2n+1)\frac{\lambda}{4}=(2n+1)\frac{v}{4f}\) (L là chiều dài dây)
\(\Rightarrow n=\frac{1}{2}(\frac{4fL}{v}-1)\)
Do f từ 80Hz đến 120 Hz nên ta tìm được n thỏa mãn sẽ từ 12 đến 17
Do đó có 6 tần số có thể tạo sóng dừng trên dây.
2. Điều chỉnh C để công suất cực đại --> Cộng hưởng xảy ra ---> \(P=\dfrac{U^2}{R}=600(W)\)
Điều chỉnh C = C2 thì công suất sẽ là: \(P_2=\dfrac{U^2}{R}\cos^2(\varphi)=600.(\dfrac{\sqrt 3}{2})^2=450W\)

chọn đáp án B
Ta có sóng dừng hai đầu cố định
l = k λ 2 = k v 2 f → f = k v 2 l = 9 , 6 k ; 93 H < f < 100 ⇒ 9 , 68 < k < 10 , 41
k thuộc Z nên ta có k=10, f=96 Hz