Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khoảng cách từ A là nút đến B là bụng gần nhất là:
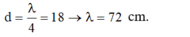
- Vì M cách B 12 cm nên MA = 6 cm.
→ Độ lệch pha của A và M là :
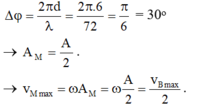
- Khoảng thời gian để độ lớn vận tốc của B nhỏ hơn vận tốc cực đại của M tương ứng với góc quét 120°
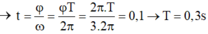
- Tốc độ truyền sóng là:


+ Khoảng cách từ A là nút đến B là bụng gần nhất là:
d = λ 4 = 18 → λ = 72 cm
+ Vì M cách B 12 cm nên MA = 6 cm.
→ Độ lệch pha của A và M là ∆ φ = 2 π d λ = 2 π . 6 72 = π 6 = 30 0 → A M = A 2
+ v M m a x = ω A M = ω A 2 = v B m a x 2
+ Khoảng thời gian để độ lớn vận tốc của B nhỏ hơn vận tốc cực đại của M tương ứng với góc quét 1200
→ t = φ ω = φ T 2 π = 2 π . T 3 . 2 π = 0 , 1 → T = 0 , 3 s
+ Tốc độ truyền sóng là: v = λ T = 72 0 , 3 = 240 cm/s = 2,4 m/s
Đáp án C

Chọn đáp án D
+ Vì A là nút gần bụng B nhất nên A B = λ 4 = 18 ⇒ λ = 72 c m
+ Ta có: A M = 18 − 12 = 6 m = λ 12 ⇒ A M = A b u n g 2 ⇒ v M − m a x = ω A M = ω A b u n g 2
+ Thời gian để v B ≤ v M − m a x ⇔ − ω A b u n g 2 ≤ v B ≤ ω A b u n g 2
⇒ Δ t = 4. T 12 = T 3 = 0 , 1 ⇒ T = 0 , 3 s ⇒ v = λ T = 240 c m / s = 2 , 4 m / s
+ Ta có: i = λ D a = 2 m m ⇒ L 2 i = 49 , 6 4 = 12 , 4 ⇒ k = 12 p = 4 ⇒ N s = 2 k + 1 = 25 N t = 2 k = 24

Đáp án B
+ Khoảng cách giữa một bụng và một nút gần nhất là λ = 7 cm
+ Biên độ dao động của điểm cách bụng B một đoạn 12 cm được xác định bởi:
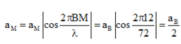
![]()
→ Khoảng cách thời gian trong một chu kì tốc độ của B nhỏ hơn tốc độ cực đại của M là
∆ t = T 3 = 0 , 1 s ⇒ T = 0 , 3 s
→ Tốc độ truyền sóng v = λ T = 2 , 4 m / s

Đáp án A
Phương pháp: Sử dụng sự tương tự giữa chuyển động tròn và dao động điều hòa, viết phương trình dao động của phần tử M
Cách giải:
Ta có: AB = 18 ⇒ λ 4 = 18 ⇒ λ = 18 . 4 = 72 c m
Khoảng cách từ điểm M đến nút A là : MA = AB – BM = 18 – 12 = 6 cm
Gọi A0 = 2a là biên độ dao động tại bụng sóng. Biên độ của M là:
A M = A 0 sin ( 2 π d λ ) = A 0 sin π 2 . 6 72 = A 0 sin π 6 = A 0 2
Tốc độ dao động cực đại của phần tử tại M là : v M m a x = ω . A M = ω . A 0 2 = v B m a x 2
Bài toán trở thành tìm khoảng thời gian trong 1 chu kỳ dao động của B mà vận tốc thỏa mãn điều kiện: v B ≤ v B m a x 2
Sử dụng đường tròn ta xác định được : sin α = 1 2 ⇒ α = 30 0
∆ t = 120 0 360 0 . T = 1 3 T ⇒ T = 0 , 2 . 3 = 0 , 6 s
Mà: λ = 72 c m ⇒ v = λ T = 72 0 , 6 = 120 c m = 1 , 2 m




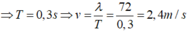
Gọi biên độ của bụng sóng là A.
Biên độ của M là: \(A_M=A.\sin(\dfrac{2\pi . 6}{48})=\dfrac{A\sqrt 2}{2}\)
V V M N P Q O v M A
Tốc độ của A nhỏ hơn tốc độ cực đại của M ứng với véc tơ quay từ N đến P và Q đến M.
Suy ra thời gian: \(t=T/2=0,1\Rightarrow T = 0,2s\)
Tốc độ truyền sóng: \(v=\dfrac{\lambda}{T}=240(cm/s)\)