Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
1: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔABC có
BN.CM là các đường cao
BN cắt CM tại H
Do đo: H là trực tâm
=>AH vuông góc với BC
2: góc EMO=góc EMH+góc OMH
=góc EHM+góc OCM
\(=90^0-\widehat{BAH}+\dfrac{180^0-\widehat{MOC}}{2}\)
\(=90^0-\widehat{BCM}+90^0-\dfrac{1}{2}\widehat{MOC}\)
=90 độ
=>ME là tiếp tuyến của (O)

(d1): y = 1/2x + 2
và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
(d1) là đường thẳng đi qua hai điểm (0; 2) và (-4; 0)
(d2) là đường thẳng đi qua hai điểm (0; 2) và (2;0)
2. Tính chu vi và diện tích của tam giác ABC
(d1) và (d2) cùng cắt nhau tại một điểm trên trục tung có tung độ bằng 2
Áp dụng định lý Pi ta go cho các tam giác AOC và BOC vuông ở O ta được:
\(AC=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}\)
\(BC=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
Chu vi tam giác ABC : AC + BC + AB= 2√5 + 2√2 + 6
≈ 13,30
Diện tích tam giác ABC
\(\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6CM^2\)
NHÉ THAK NHÌU

a, HS Tự làm
b, Tìm được C(–2; –3) là tọa độ giao điểm của d 1 và d 2
c, Kẻ OH ⊥ AB (CH ⊥ Ox)
S A B C = 1 2 C H . A B = 9 4 (đvdt)

a: Tọa độ A là:
y=0 và -1/2x+4=0
=>x=8 và y=0
=>A(8;0)
Tọa độ B là;
y=0 và -x+4=0
=>x=4 và y=0
=>B(4;0)
Tọa độ C là;
1/2x+4=-x+4 và y=-x+4
=>x=0 và y=4
=>C(0;4)
b: A(8;0); B(4;0); C(0;4)
\(AB=\sqrt{\left(4-8\right)^2+\left(0-0\right)^2}=4\)
\(AC=\sqrt{\left(0-8\right)^2+\left(4-0\right)^2}=4\sqrt{5}\)
\(BC=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{2}{\sqrt{5}}\)
=>\(sinBAC=\dfrac{1}{\sqrt{5}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot4\cdot4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=8\)
\(C=4+4\sqrt{5}+4\sqrt{2}\)

Bài 12:
a:
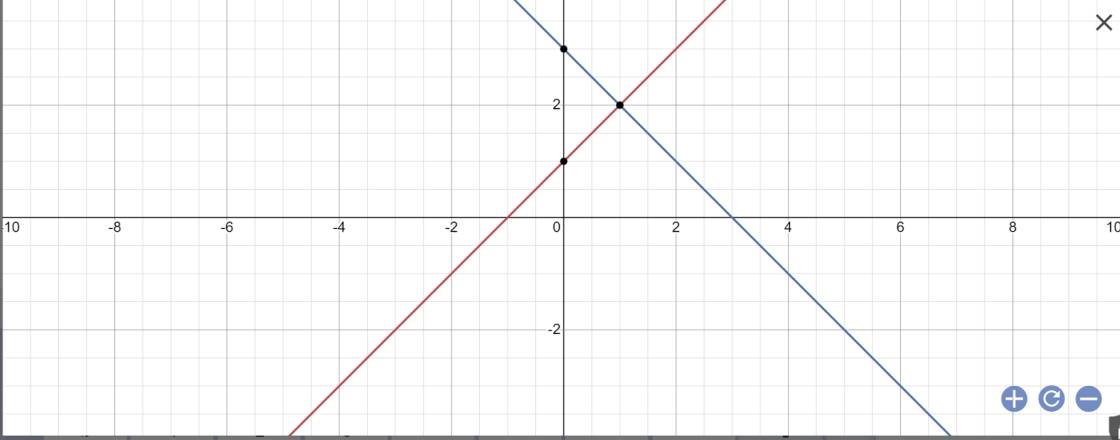
b: Phương trình hoành độ giao điểm là:
x+1=-x+3
=>x+x=3-1
=>2x=2
=>x=1
Thay x=1 vào y=x+1, ta được:
\(y=1+1=2\)
Vậy: (d1) cắt (d2) tại A(1;2)
c: Để (d1) cắt (d3) tại một điểm nằm trên trục tung thì
\(\left\{{}\begin{matrix}m\ne1\\m-1=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2
d: Thay x=1 và y=2 vào (d3), ta được:
\(m+m-1=2\)
=>2m-1=2
=>2m=1+2=3
=>\(m=\dfrac{3}{2}\)
Vậy: Khi m=3/2 thì ba đường thẳng (d1),(d2),(d3) đồng quy
Bài 4:
1: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔABC có
BN.CM là các đường cao
BN cắt CM tại H
Do đo: H là trực tâm
=>AH vuông góc với BC
2: góc EMO=góc EMH+góc OMH
=góc EHM+góc OCM
\(=90^0-\widehat{BAH}+\dfrac{180^0-\widehat{MOC}}{2}\)
\(=90^0-\widehat{BCM}+90^0-\dfrac{1}{2}\widehat{MOC}\)
=90 độ
=>ME là tiếp tuyến của (O)