Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Động năng ban đầu cực đại của quang electron bứt ra từ mặt quả cầu:
\(\frac{mv^2_{max}}{2}=\frac{hc}{\lambda}-A=2,7.10^{-19}J\)
Gọi Q là điện tích của quả cầu, điện tích này phải là điện tích dương để giữ electron; điện tích Q phân bố đều trên mặt quả cầu, do đó điện thế trên mặt quả cầu là:
\(V=9.10^9.\frac{Q}{R}\). Trên quả cầu hình thành điện trường với các đường sức vuông góc với mặt cầu và hướng ra ngoài ( vì Q>0), điện trường này ngăn cản electron thoát ra khỏi quả cầu, công của điện trường cản là: \(W=eV=9.10^9.\frac{Qe}{R}\)
Muốn cho electron không thoát ra , công đó phải bằng động năng ban đầu cực đại của electron nghĩa là: \(9.10^9.\frac{Qe}{R}=\frac{mv^2_{max}}{2}\)
Thay số ta rút ra : \(Q=1,9.10^{-11}C\)


Đáp án là B
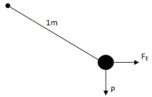
Lực căng dây là tổng hợp lực của P và E
P=m.g=1,962N
FE=E.q=2N
T=P2+F2E=>T=2.8N»2.21/2

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

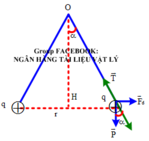
Các lực tác dụng lên vật
+ Trọng lực P → (thẳng đứng hướng xuống)
+ Lực điện F → d (hai điện tích giống nhau nên hai điện tích đẩy nhau)
+ Lực căng T →
+ Khi quả cầu cân bằng ta có: T → + F → + P → = 0
+ Từ hình vẽ ta có: tan α = F P
Chọn đáp án C