Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

30 phút = (1/2) giờ
Gọi quãng đường AB là x (km). Điều kiện x > 0.
Thời gian xe máy đi từ A đến B là x/30 (giờ).
Thời gian xe máy đi từ B về A là x/24 (giờ).
Ta có phương trình:
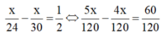
⇔ 5x - 4x = 60 ⇔ x = 60 (thỏa mãn điều kiện)
Vậy quãng đường AB là 60 km.

Gọi độ dài quãng đường AB là x(km), (x>0)
khi đó: thời gian khi đi từ A đến B là\(\)x/4(h)
thời gian đi từ B về A là x/5 (h)
do thời gian lúc về ít hơn thời gian đi là 30' tức 1/2 h nên ta có phương trình x/5 -x/4 =1/2
Đổi 30 phút = 1/2giờ
Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x>0 ). Thời gian xe đi từ A đến B là 24/x (giờ).
Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là 24/x+4 (giờ) Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:
\(\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}\). Giải phương trình:
\(\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}\Leftrightarrow x^2+4x-192=0\Leftrightarrow\orbr{\begin{cases}x=12\\x=-16\end{cases}}\)
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.

Gọi độ dài quãng đường AB là x(km)(Điều kiện: x>0)
Thời gian người đó đi từ A đến B là: \(\dfrac{x}{45}\left(h\right)\)
Thời gian người đó đi từ B về A là: \(\dfrac{x}{50}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{45}-\dfrac{x}{50}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{10x}{450}-\dfrac{9x}{450}=\dfrac{180}{450}\)
\(\Leftrightarrow x=180\left(nhận\right)\)
Vậy: Độ dài quãng đường AB là 180km

gọi độ dài quãng đường AB là x(km)(x>0)
độ dài quãng đường khác là x+15(km)
thời gian đi là: \(\frac{x}{30}\left(h\right)\)
thời gian về là:\(\frac{x+15}{40}\left(h\right)\)
theo đề bài: thời gian về ít hơn thời gian đi là 20 phút\(=\frac{1}{3}h\) nên ta có PT
\(\frac{x}{30}-\frac{x+15}{40}=\frac{1}{3}\)
\(\Leftrightarrow\frac{4x}{120}-\frac{3\left(x+15\right)}{120}=\frac{40}{120}\)
\(\Leftrightarrow4x-3x-45=40\)
\(\Leftrightarrow x=95\left(tmđk\right)\)
vậy đọ dài quãng đường AB là 95 km
Đổi: 20 phút = 1/3 h Gọi quãng đường AB là x (km) (x>0) Thời gian lúc đi là: x/30 (h) QĐ lúc về là: x + 15 (km) Thời gian lúc về là: (x + 15)/40 (h) Vì thời gian về ít hơn thời gian đi 20 phút nên ta có PT: x/30 - (x+15)/40 = 1/3 => ( x - 45)/120 = 1/3 => x - 45 = 40 => x = 85 (km) Vậy quãng đường AB dài 85 km

Gọi quãng đường AB là x(x>0)x(x>0)
Thời gian đi: x45x45
Thời gian về: x40x40
Đổi: 1010 phút=1616 giờ
Theo bài ra ta có phương trình:
x40−x45=16⇔270x−240x=1800⇔30x=1800⇔x=60 (thoả mãn)x40−x45=16⇔270x−240x=1800⇔30x=1800⇔x=60 (thoả mãn)
Vậy quãng đường dài: 60 km
Gọi quãng đường AB là x ( x > 0, km )
Thời gian người đó đi xe máy từ A -> B là : \(\frac{x}{45}\)giờ
Thời gian người đó đi từ B -> A là : \(\frac{x}{40}\)giờ
vì thời gian về nhiều hơn đi là 10 phút = \(\frac{1}{6}\)giờ
nên ta có phương trình : \(\frac{x}{40}-\frac{x}{45}=\frac{1}{6}\Leftrightarrow x=60\)
Vậy quãng đường AB là 60 km

đổi 12 phút = 0,2 giờ
gọi độ dài quãng đường AB là: x (đơn vị:km,x>0)
=> thời gian mà xe máy đi từ A đến B là: `x/35` (giờ)
=> thời gian mà xe máy đi từ B đến A là: `x/40` (giờ)
vì thời gian về ít hơn thời gian đi 12 phút nên ta có phương trình sau
\(\dfrac{x}{35}-\dfrac{x}{40}=0,2\\ < =>x\cdot\left(\dfrac{1}{35}-\dfrac{1}{40}\right)=0,2\\ < =>x\cdot\dfrac{1}{280}=0,2\\ < =>x=56\left(tm\right)\)
vậy độ dài quãng đường AB là 56km
\(12p=0,2h\)
Gọi \(x\left(km\right)\) là quãng đường AB \(\left(x>0\right)\)
Theo bài, ta có pt :
\(\dfrac{x}{35}=\dfrac{x}{40}+0,2\)
\(\Leftrightarrow\dfrac{x}{35}-\dfrac{x}{40}-0,2=0\)
\(\Leftrightarrow\dfrac{40x-35x-280}{1400}=0\)
\(\Leftrightarrow5x=280\)
\(\Leftrightarrow x=56\left(tmdk\right)\)
Vậy quãng đường AB dài 56km

Gọi quãng đường AB là x(x>0)km
thời gian đi từ A đến B là \(\dfrac{x}{15}\)h
thời gian về từ B về A là \(\dfrac{x}{12}h\)
vì thời gian về lâu hơn thời gian đi là 30p =\(\dfrac{1}{2}\)h nên ta có pt
\(\dfrac{x}{12}\)-\(\dfrac{x}{15}\)=\(\dfrac{1}{2}\)
giải pt x=30 TM
vậy quãng đường AB dài 30 km

Gọi quãng đường AB là x (km, x>0)
Người đó đi xe đạp từ A đến B với vận tốc 15km/h
\(\to\) Thời gian lúc đi của người đó là \(\dfrac{x}{15}\) (h)
Người đó đi xe đạp từ B về A với vận tốc 12km/h
\(\to\) Thời gian lúc về của người đó là \(\dfrac{x}{12}\) (h)
Vì thời gian về nhiểu hơn thời gian đi là 30 phút
\(\to\) Ta có pt: \(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{30}{60}\)
\(\to 5x-4x=30\)
\(\to x=30\) (TM)
Vậy quãng đường AB là 30km

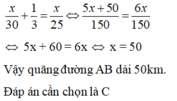
Lời giải:
Đổi 3h40 phút bằng $\frac{11}{3}$ giờ
Thời gian đi là: $\frac{AB}{24}$ (giờ)
Thời gian về là: $\frac{AB}{30}$ (giờ)
Tổng thời gian đi và về là:
$\frac{AB}{24}+\frac{AB}{30}=\frac{11}{3}$
$\Leftrightarrow \frac{3}{40}.AB=\frac{11}{3}$
$\Leftrightarrow AB=\frac{440}{9}$ (km)
Số giờ để người đó đi từ A đến B là:
3 giờ 40 phút : 2 = 1 giờ 50 phút
Đổi 1 giờ 50 phút = 11/6 giờ
Tổng vận tốc 2 xe là :
24 + 30 = 54 (km/giờ)
Quãng đường AB dài là:
54 x 11/6 = 99 (km)
Đáp số: ... km
bài giải đây bạn nha!!!