Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian đi hai quãng đường của hai xe là:
\(t_1=\dfrac{0,3AB}{v_1};t_2=\dfrac{0,3AB}{v_2}\)
Phúc đến xe buýt chậm 3 phút nên: \(t_1-t_2=\dfrac{3}{60}\)
\(\Rightarrow\dfrac{0,3AB}{v_1}-\dfrac{0,3AB}{v_2}=\dfrac{1}{20}\)\(\Rightarrow\dfrac{AB}{v_1}-\dfrac{AB}{v_2}=\dfrac{1}{6}\)
Thời gian người đó phải chờ là:
\(t=\dfrac{0,7AB}{v_1}-\dfrac{0,7AB}{v_2}=0,7\cdot\left(\dfrac{AB}{v_1}-\dfrac{AB}{v_2}\right)=0,7\cdot\dfrac{1}{6}=\dfrac{7}{60}\left(h\right)=7phút\)

ta có:
gọi thời gian taxi đi 2/3 đoạn đường đầu là t
\(\Rightarrow\) thời gian đi 2/3 đoạn đường đầu là t+1/3
ta lại có:
thời gian taxi đi 1/3 đoạn đường còn lại là:
\(t'=\frac{t}{2}\) do quãng đường tỉ lệ thuận với thời gian(do vận tốc taxi ko đổi)
từ đó suy ra thời gian xe buýt đi 1/3 đoạn đường còn lại là:
\(t''=\frac{3t+1}{6}\)
vậy thời gian người đó phải đợi ở B là:
\(\Delta t=t''-t'=\frac{3t+1}{6}-\frac{t}{2}\)
\(\Leftrightarrow\Delta t=\frac{3t+1-3t}{6}=\frac{1}{6}h=10'\)
vậy thời gian người đó phải chờ là 10 phút
bài này mjk nghĩ chưa đủ điều kiện để giải, bn có chắc ghi đúng đề?

B1 :
Làm tương tự thế này nha :
Gọi C là điểm xe ta xi đuổi kịp xe buýt, t là thời gian taxi đi đoạn AC:
AC = 1/3AB; CB = 2/3AB; AC = 1/2 CB
Thời gian xe búyt đi đoạn AC: t+ 20 (phút)
thời gian mỗi xe đi tỉ lệ với quãng đương đi được của chúng,nên:
thời gian xe taxi đi đoạn CB: t/2 ( phút)
thời gian xe buýt đi đoạn CB: t+20/2 = t/2+ 10 ( phút)
=> thời gian người đó phải đợi xe buýt ở bến B: = (t/2 +10) - t/2 = 10 phút
B3:
Gọi C là điểm xe ta xi đuổi kịp xe buýt, t là thời gian taxi đi đoạn AC:
AC = 1/3AB; CB = 2/3AB; AC = 1/2 CB
Thời gian xe búyt đi đoạn AC: t+ 20 (phút)
thời gian mỗi xe đi tỉ lệ với quãng đương đi được của chúng,nên:
thời gian xe taxi đi đoạn CB: t/2 ( phút)
thời gian xe buýt đi đoạn CB: t+20/2 = t/2+ 10 ( phút)
=> thời gian người đó phải đợi xe buýt ở bến B: = (t/2 +10) - t/2 = 10 phút

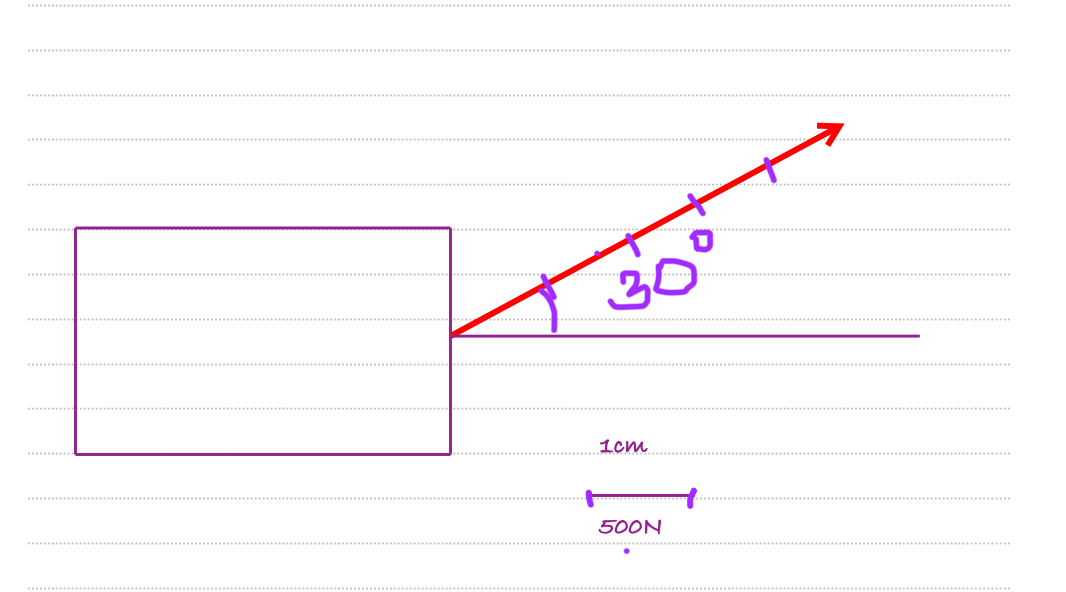
c)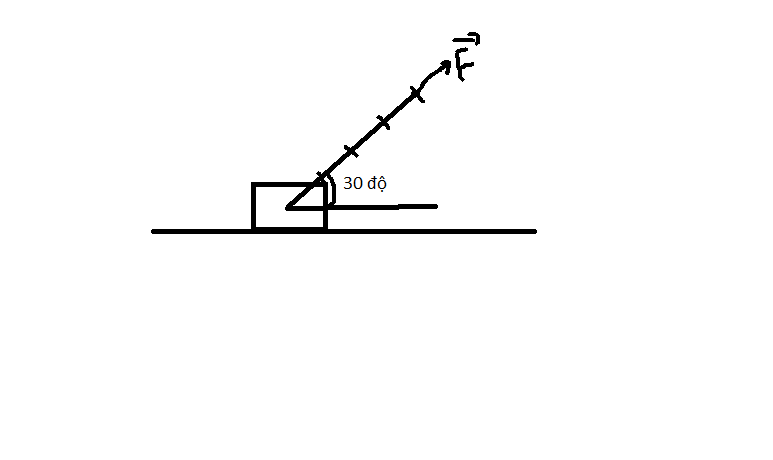
Điểm đặt tại tâm vật.
Chiều hướng lên so với mặt phẳng nghiêng góc 30 độ.
Độ lớn: \(F=500N\)

Gọi quãng đường đi từ nhà đến trường là AC, từ nhà đến trạm xe là AB, từ trạm xe đến trường là BC
Ta có
\(t_1=\frac{AB}{12}\)
\(t_2=15'=\frac{1}{4}h\)
\(t_3=\frac{AC-AB}{30}=\frac{24-AB}{30}\)
Nếu đạp xe từ nhà đến trường thì mất:
\(t'=\frac{24}{12}=2\left(h\right)\)
Mà
\(t_1+t_2+t_3\)= 2-0,5
\(\frac{AB}{12}+\frac{24-AB}{30}+\frac{1}{4}=1,5\)
=> AB=18 (km)
Thời gian sinh viên đã đi xe buýt là
\(t_4=\frac{24-18}{30}=\frac{1}{5}=0,2\left(h\right)\)
sai rồi bạn ơi \(\dfrac{AB}{12}+\dfrac{24-AB}{30}+\dfrac{1}{4}=1.5\)
=>AB=9km
Vậy mới đúng![]()


Bài làm
Gọi C là điểm xe taxi đuổi kịp xe buýt, t là thời gian taxi đi đoạn AC:
AC = \(\dfrac{1}{3}\)AB; CB = \(\dfrac{2}{3}\)AB; AC = \(\dfrac{1}{2}\)CB
Thời gian xe búyt đi đoạn AC: t + 20(phút)
Thời gian mỗi xe đi tỉ lệ với quãng đương đi được của chúng nên:
Thời gian xe taxi đi đoạn CB: \(\dfrac{t}{2}\)( phút)
Thời gian xe buýt đi đoạn CB: t + \(\dfrac{20}{2}\) = \(\dfrac{t}{2}\) + 10( phút)
=> Thời gian người đó phải đợi xe buýt ở bến B là: (\(\dfrac{t}{2}\) +10) - \(\dfrac{t}{2}\) = 10(phút).