Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi A là biến cố “Rút được đề thi có 4 câu đã học thuộc”, ta lần lượt có
Vì ngân hàng câu hỏi có 100 câu và mỗi đề thi có 5 câu nên có
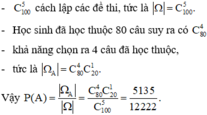

Đáp án B.
+ Rút ra 4 câu bất kì =>Có C 50 4 cách.
+ Rút ra 4 câu mà không có câu nào học thuộc =>Có C 30 4 cách.
Xác suất để bạn đó rút được 4 câu trong đó có ít nhất một câu đã học là 1 − C 30 4 C 50 4

Chọn đáp án C.
* TH1: Đề thi gồm 1 câu lý thuyết và 2 câu bài tập
Số cách tạo đề thi: C 4 1 . C 6 2 cách
* TH2: Đề thi gồm 2 câu lý thuyết và 1 câu bài tập
Số cách tạo đề thi: C 4 2 . C 6 1 cách
* KL: Số cách tạo đề thi: C 4 1 . C 6 2 + C 4 2 . C 6 1 = 96 cách

Phương pháp
Sử dụng quy tắc cộng để làm bài toán.
Cách giải
Để chọn được 3 câu hỏi trong đó có ít nhất 1 câu lý thuyết và 1 câu bài tập ta chia thành 2 TH:
TH1: Chọn 1 câu lý thuyết và 2 câu bài tập có: C 4 1 . C 6 2 cách chọn.
TH2: Chọn 2 câu lý thuyết và 1 câu bài tập có: C 4 2 . C 6 1 cách chọn.
Như vậy có: C 4 1 . C 6 2 + C 4 2 . C 6 1 = 96 cách chọn.
Chọn C.

Đáp án B
Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng nhiều hơn 2 trong 5 câu còn lại. Xác suất mỗi câu chọn đúng là 1 4 và không chọn đúng là 3 4 .
Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng hoặc 3 hoặc 4 hoặc 5 trong 5 câu còn lại.
Do đó xác suất cần tìm là ![]()

Chọn đáp án D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố học sinh chỉ chọn đúng đáp án của 25 câu hỏi
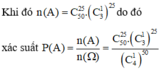



Đáp án A
Số cách sắp xếp 50 câu cho một đề thi là 50!
Số cách chọn 20 câu nhận biết để xếp chúng vào đầu tiên là: 20!
Số cách chọn 10 câu thông hiểu để xếp chúng vào vị trí thứ hai là 10!
Số cách chọn 15 câu vận dụng để xếp chúng vào vị trí thứ ba là 15!
Số cách chọn 5 câu vận dụng cao xếp chúng vào vị trí cuối cùng là 5!
Xác suất cần tìm được tính bằng: P = 20 ! 10 ! 15 ! 5 ! 50 ! = 4 , 56 . 10 - 26
Chọn phương án A