Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án C
Giả sử ở thời điểm t nào đó ta có như trên VTLG
Giả sử suất điện động xuất hiện trong khung dây có dạng
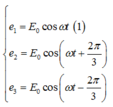
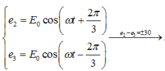
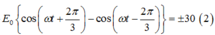
Áp dụng công thức toán học 
Phương trình (2) được viết lại:
![]() . Kết hợp với (1) ta có
. Kết hợp với (1) ta có
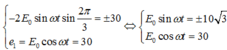
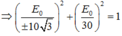
![]()

Đáp án D
Suất điện động trong các cuộn dây có dạng: 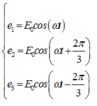
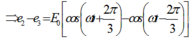
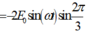
Theo giả thiết của bài toán
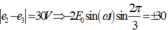
Kết hợp ![]()

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

GIẢI THÍCH: Suất điện động xuất hiện trong các cuộn dây có dạng:
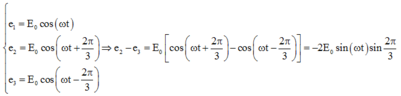
Theo giả thuyết của bài toán
![]()
Kết hợp với
![]()
Chọn C.

Suất điện động cảm ứng trong khung: \(e=-\phi'_{(t)}\)
\(\Rightarrow e=14,4.\sin(720t+\dfrac{\pi}{6})(V)\)
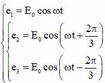
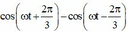
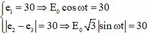



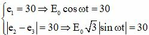
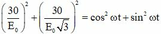

Chọn đáp án C
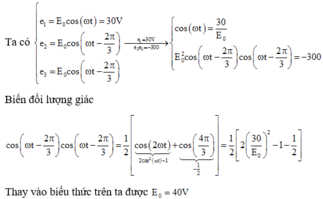
+ ta có: e 1 = E 0 cos ω t e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 ⇒ e 2 − e 3 = E 0 cos ω t + 2 π 3 − cos ω t − 2 π 3
+ Lại có: cos ω t + 2 π 3 − cos ω t − 2 π 3 − 2 sin ω t . sin π 3 = − 3 sin ω t ⇒ e 2 − e 3 = E 0 3 sin ω t
+ Theo đề: e 1 = 30 ⇒ E 0 cos ω t = 30 e 2 − e 3 = 30 ⇒ E 0 3 sin ω t = 30 ⇒ 30 E 0 2 + 30 E 0 3 2 = cos 2 ω t + sin 2 ω t .
⇒ 30 E 0 2 + 30 E 0 3 2 = 1 ⇒ E 0 = 20 3 V ≈ 34 , 64 V