Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc tọa độ O tại vị trí electron bắt đầu vào vùng điện trường, hệ tọa độ xoy có dạng như hình vẽ:
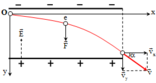
Thành phần Ox chuyển động thẳng đều: x = v 0 t
Thành phần Oy chuyển động nhanh dần đều: y = 1 2 a y t 2
Vậy phương trình quỹ đạo của elctron là: y = 1 2 a y x v 0 2
Lực điện trường tác dụng lên electron: F → = q E → = m a → → F x = m a x = 0 F y = m a y = F
a x = 0 a y = F m = q E m = q U m d → x = v 0 t = 2.10 7 t y = 1 2 a y x v 0 2 = 1 2 q U m d v 0 2 x 2 = 2 x 2
a. Vậy phương trình quỹ đạo có dạng: y = 1 2 a y x v 0 2 = 1 2 q U m d v 0 2 x 2 = 2 x 2
b. Tính quãng đường electron đi được theo phương Ox khi nó ra khỏi tụ.
Dựa theo thành phần nằm ngang Ox ta có: x = l = 5.10 − 2 m
c. Vận tốc electron khi rời khỏi tụ:
v x = v 0 v y = v 0 y + a y t → x = v 0 t → t = x v 0 v x = 2.10 7 v y = 0 +...

a) hai điện tích như nhau=> hai điện tích có độ lớn bằng nhau=> |q1|=|q2|=q
Và hai điện tích đẩy nhau nên hai điện tích cùng dấu.
\(F_1=\frac{k.\left|q_1.q_2\right|}{r^2}\Leftrightarrow10^{-5}=\frac{9.10^9.\left|q^2\right|}{\left(0,04\right)^2}\Rightarrow q=1,33.10^{-9}C\)
b) \(\frac{F_1}{F_2}=\frac{r_2^2}{r_1^2}\Leftrightarrow\frac{10^{-5}}{2,5.10^{-6}}=\frac{r_2^2}{0,o4^2}\Rightarrow r_2\approx0,08m=8cm\)

Chọn C.
Độ lớn điện tích mỗi hạt bụi:
![]()
Lực tương tác Cu-lông:
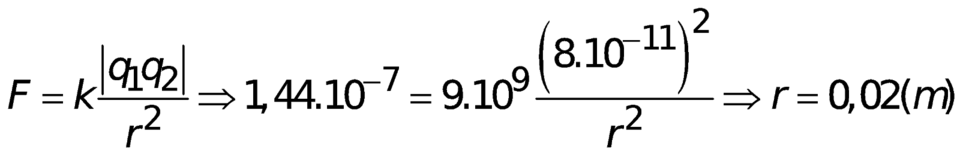

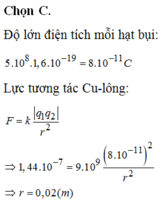


Vì trong nguyên tử còn có hạt nhân mang điện tích dương, lực tương tác tĩnh điện giữa hạt nhân và electron đủ lớn để giữ cho electron không bị bay ra khỏi mẩu sắt.