Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Áp dụng bảo toàn năng lượng trong mạch LC
Cách giải:
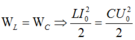
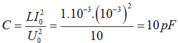

Áp dụng bảo toàn năng lượng toàn phần của mạch LC ta có: \(W=\frac{1}{2}Cu^2+\frac{1}{2}Li^2=\frac{1}{2}CU_0^2\)
\(\Rightarrow Li^2=C\left(U_0^2-u^2\right)\)
\(\Rightarrow i=\sqrt{\frac{C}{L}\left(U_0^2-u^2\right)}\)
Thay số ta được i = 6mA.
Đáp án C.

\(C = \frac{1}{\omega^2.L}= 5.10^{-6}F.\)
\(U_0 = \frac{q_0}{C}= \frac{I_0}{C.\omega}= \frac{I_0.\sqrt{L}}{\sqrt{C}} = 8V.\)
\(i = I = \frac{I_0}{\sqrt{2}}. \)
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{u}{U_0}\right)^2 = 1- \left(\frac{i}{I_0}\right)^2 = 1 - \frac{1}{2}= \frac{1}{2}\)
=> \(u = \frac{1}{\sqrt{2}}U_0= 4\sqrt{2}V.\)
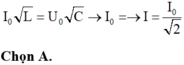


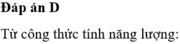
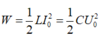
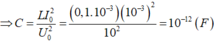
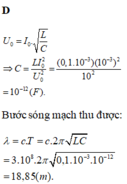
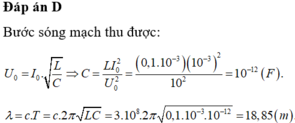
Đáp án B
+ Ta có: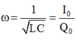
+ Mà Q0 = C.U0