Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
W L = 1 8 W C W L = 1 9 W ⇒ i = 1 9 I 0 = 3 ( m A ) W C = 8 9 W

Thời gian để cường độ dòng điện giảm từ cực đại xuống nửa cực đại là T/6, suy ra:
\(\dfrac{T}{6}=\dfrac{8}{3}\Rightarrow T = 16\mu s=16.10^{-6}s\)
Ở thời điểm cường độ trong mạch bằng 0 thì điện tích trong mạch cực đại, suy ra:
\(q=Q_0=\dfrac{I_0}{\omega}=\dfrac{I_0.T}{2\pi}=\dfrac{2,22.16.10^{-6}}{2\pi}=5,65.10^{-6}(C)=5,65 \mu C\)

\(W_L+W_C = W_{Cmax}\)
mà \(W_{d} = 2 W_t\) => \(W_{Cmax} = \frac{3}{2}W_C=> \frac{1}{2}CU_0^2 = \frac{3}{2}.\frac{1}{2}Cu^2.\)
=> \(u^2 = \frac{2}{3}U_0^2=> u = \pm \frac{2\sqrt{2}}{\sqrt{3}} \approx \pm 1,63 V.\)
Chọn đáp án \(D.1,63V.\)

Chú ý trong mạch dao động \(i_1\perp u_1;i_2\perp u_2\)
Mặt khác ta có độ lệch pha giữa hai \(i_1;i_2\):\(t_2-t_1=\frac{\pi}{2}\sqrt{LC}=\frac{T}{4}\Rightarrow\Delta\varphi=\frac{T}{4}.\frac{2\pi}{T}=\frac{\pi}{2}\)
=> \(i_1\perp i_2\)
i i u u 1 1 2 2
Nhìn vào đường tròn ta thấy \(i_1\perp i_2,u_1\perp u_2\); \(i_1\) ngược pha \(u_2\) và ngược lại.
\(\frac{i_1^2}{I^2_0}+\frac{u^2_1}{U_0^2}=1;\frac{i_1^2}{I^2_0}+\frac{i^2_2}{I_0^2}=1;\frac{i_1^2}{I^2_0}+\frac{u^2_2}{U_0^2}=1;\frac{i_2^2}{I^2_0}+\frac{u^2_1}{U_0^2}=1;\)
\(U_0=\frac{I_0}{\omega}\Rightarrow I_0=\omega\sqrt{U_0}=\frac{1}{\sqrt{LC}}\sqrt{U_0}\)
Dựa vào các phương trình trên ta thấy chỉ có đáp án D là sai.
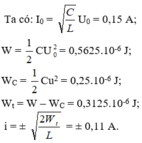
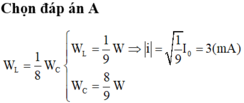

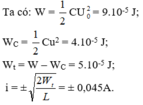
Đáp án C