Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Sau khi kéo vật B xuống dưới 20 cm và thả nhẹ thì hệ dao động với biên độ 20cm.
∆l12 = m12g/k = 0,1m = 10cm
Vật B đi lên được h1 = 30 cm thì lực đàn hồi của lò xo triệt tiêu (x12 = -10cm = -A/2). Khi đó vận tốc của B
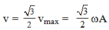
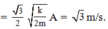
Sau đó vận tốc của vật A có độ lớn giảm dần (vì đang đi về biên trên),
Vật B đi lên thêm được độ cao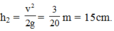
+ Vật B đổi chiều chuyển động khi khi lên được độ cao h = h1 + h2 = 45cm = 0,45m
+ Khoảng thời gian từ khi vậ B tuột khỏi dây nối đến khi rơi đến vị trí thả ban đầu là:
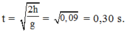

Đáp án A
Sau khi kéo vật B xuống dưới 20 cm và thả nhẹ thì hệ dao động với biên độ 20cm.
Vật B đi lên được h1 = 30 cm thì không chịu tác dụng của lực đàn hồi của lò xo nữa. Khi đó vận tốc của B có độ lớn:
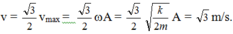
Vật B đi lên thêm được độ cao h2 v 2 2 g = 3 20 m = 15 c m
Vật B đổi chiều chuyển động khi lên được độ cao h = h1 + h2 = 45cm = 0,45m
Khoảng thời gian từ khi vậ B tuột khỏi dây nối đến khi rơi đến vị trí thả ban đầu là t= 2 h g = 0 , 09 = 0 , 30 s

Đáp án A
![]()
Ban đầu hệ hai vật dao động với biên độ:
A = 9,66 – 4= 4 2 c m ;
Xét các lực tác dụng vào vật B: mBg – T = mBa =>
T = mB(g – a)= mB (g + ω 2 x )
Dây còn căng khi T ≥ 0
![]()
Vậy cả 2 vật cùng chuyển động từ biên dương đến vị trí có li độ x = - 4 hết thời gian
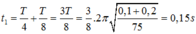
Tại x = - 4 cm, 2 vật có cùng vận tốc
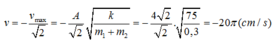
Từ x = -4 cm thì vật mA đi lên chậm hơn mB nên dây sẽ trùng.
Khi đó mA nhận OA làm VTCB mới, cách vị trí đoạn ∆ l O A = 4 3 c m nên mA dao động với biên độ
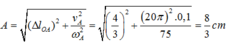
Thời gian mA đi từ x1 đến biên âm của nó là :
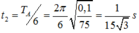
Thời gian cần tìm là t = t1 + t2 = 0,1885 s

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Chọn gốc toạ độ tại VTCB; chiều dương hướng xuống dưới.
Độ giãn của hệ lò xo + dây đàn hồi khi vật ở VTCB:
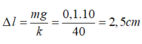
- Khoảng thời gian từ khi thả vật đến khi vật đạt độ cao cực đại lần thứ nhất được chia làm hai giai đoạn:
+ Giai đoạn 1 (sợi dây bị kéo giãn tương đương như một lò xo): Vật đi từ vị trí biên x = 5cm đến vị trí x = -∆l = -2,5cm
+ Giai đoạn 2 (khi dây bị trùng lực đàn hồi bị triệt tiêu): Vật đi từ vị trị x = -∆l = -2,5cm đến biên âm.
- Giai đoạn 1:
Hệ dao động gồm lò xo và sợi dây đàn hồi nhẹ có cùng chiều dài tự nhiên treo thẳng đứng vào cùng một điểm cố định đầu còn lại của lò xo và sợi dây gắn vào vật nặng được coi như hai lò xo mắc song song
=> Độ cứng của hệ: k = k1 + k2 = 10 + 30 = 40 N/m
Chu kì dao động của hệ:
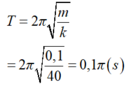
Ban đầu vật ở VTCB, kéo vật thẳng đứng xuống dưới một đoạn a = 5cm rồi thả nhẹ => A = 5cm.
Thời gian vật đi từ x = 5cm đến x = -2,5cm được biểu diễn trên đường tròn lượng giác:
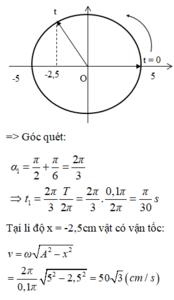
- Giai đoạn 2:
Độ giãn của lò xo ở VTCB: ∆ l ' = m g k 1 = 10 c m => tại vị trí lò xo không biến dạng x = -10cm
Vật dao động điều hoà với chu kì và biên độ:
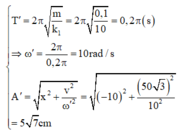
Vật đi từ vị trí x = -∆l = -10cm đến biên âm x = - 5 7 c m được biểu diễn trên đường tròn lượng giác:
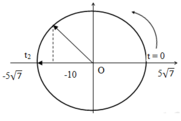
Từ đường tròn lượng giác ta tính được:
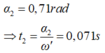
=> Khoảng thời gian kể từ khi thả vật đến khi vật đạt độ cao cực đại: t = t1 + t2 = 0,175s
Đáp án C
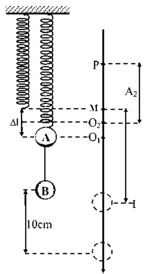


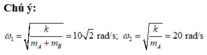
Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng O của hệ hai vật Δ l 0 = 2 m g k = 5 cm, kéo hệ xuống dưới vị trí cân bằng 10 cm rồi thả nhẹ, vậy hệ sẽ dao động với biên độ A = 10 cm.
+ Ta có thể chia quá trình chuyển động của hệ thành các giai đoạn sau:
Giai đoạn 1: Hệ hai vật dao động điều hòa quanh vị trí cân bằng O.
· Tốc độ của hai vật khi đi qua vị trí cân bằng v m a x = ω A = k 2 m A = 100 2 cm/s.
Giai đoạn 2: Chuyển động của hai vật sau khi đi qua vị trí cân bằng O.
· Khi đi qua vị trí cân bằng O, tốc độ của vật A sẽ giảm, vật B sẽ chuyển động thẳng đứng lên trên với vận tốc ban đầu bằng v m a x , do có sự khác nhau về tốc độ nên hai vật không dao động chung với nhau nữa.
· Tuy nhiên sự kiện trên chỉ diễn ra rất ngắn, vật A ngay sau đó sẽ dao động quanh vị trí cân bằng mới ở phía trên O một đoạn 2,5 cm do đó ngay lập tức tốc độ của A sẽ tăng, trong khi B lại giảm → hệ hai vật lại được xem như ban đầu và dao động quanh vị trí cân bằng O.
Giai đoạn 3: Chuyển động của hai vật sau khi dây bị chùng
· Phương trình định luật II cho vật m 2 : m 2 g − T = m 2 a , khi T = 0 dây chùng → x = − g ω 2 = − 5 cm. Lúc này v A = 3 2 v m a x = 50 6 cm/s.
· Vật dao A dao động quanh vị trí cân bằng mới O' cách vị trí cân bằng cũ một đoạn Δ l = m g k = 2 , 5 cm với biên độ A ' = 2 , 5 2 + 50 6 20 2 = 6 , 61 cm.
Từ các lập luận trên ta thấy rằng khi A dừng lại lần đầu tiên ứng với vị trí biên trên, khi đó quãng đường vật đi được sẽ là S = 10 + 5 + (6,61 – 2,5) = 19,1 cm.