

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




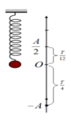
Chọn chiều dương thẳng đứng hướng lên, gốc tọa độ tại VTCB.
Biết rằng khi vật ở VTCB, lò xo bị nén một đoạn bằng A/2
Thời gian ngắn nhất kể từ khi vật ở vị trí thấp nhất đến khi lò xo không biến dạng thời gian vật đi từ li độ
(theo chiều (+) )
Mình giải thích thêm nếu bạn không hiểu nha
Biết rằng khi vật ở VTCB, lò xo bị nén một đoạn bằng A/2 tức là để lò xo không biến dạng thì vật phải qua VTCB và có li độ dương (do ta chọn chiều (+) hướng lên).
Mà do suy ra từ VTCB vật phải đi đến tọa độ
thì lò xo sẽ trở về trạng thái không biến dạng.
bạn thử vẽ hình ra sẽ thấy.

Vị trí lò xo không biến dang là \(x=-\Delta l_0\)
Vị trí cao nhất là \(x=-A\)
\(\Rightarrow\) thời gian ngắn nhất là \(\frac{T}{6}=\frac{3}{6}=0,5\left(s\right)\)

\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui