Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

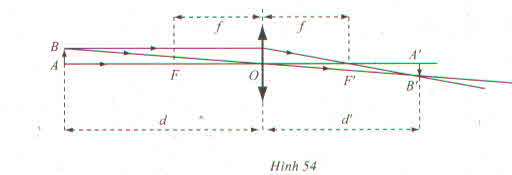
a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .

a/ Giả sử \(O_1\) là tâm của đường tròn ngoại tiếp tam giác HBC , thì \(O_1\) chính là ảnh của (O) qua phép đối xứng trục BC . Cho nên bán kính của chúng bằng nhau . Tương tự hai đường tròn ngoại tiếp của hai tam giác còn lại có bán kính bằng bán kính của (O) .
b/ Ta hoàn toàn chứng minh được \(O_1;O_2;O_3\) là các ảnh của O qua phép đối xứng trục BC,CA,AB . Vì vậy bán kính các đường tròn này bằng nhau . Mặt khác ta chứng minh tam giác ABC bằng tam giác
a/ Giả sử \(O_1\) là tâm của đường tròn ngoại tiếp tam giác HBC , thì \(O_1\) chính là ảnh của (O) qua phép đối xứng trục BC . Cho nên bán kính của chúng bằng nhau . Tương tự hai đường tròn ngoại tiếp của hai tam giác còn lại có bán kính bằng bán kính của (O) .
b/ Ta hoàn toàn chứng minh được \(O_1;O_2;O_3\) là các ảnh của O qua phép đối xứng trục BC,CA,AB . Vì vậy bán kính các đường tròn này bằng nhau . Mặt khác ta chứng minh tam giác ABC bằng tam giác \(O_1;O_2;O_3\)


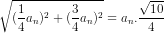 với n ε N*.
với n ε N*. 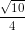


Chọn C.
Gọi tâm của quả cầu lớn là I. Tâm của 4 quả cầu nhỏ nằm bên dưới lần lượt là A, B, D, C.
Khi đó I.ABCD là hình chóp tứ giác đều và có độ dài các cạnh như hình vẽ bên dưới.