Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đề nghị khi đăng câu hỏi nên ấn 1 lần, sau ns sẽ hiện ra, tốn S ==

TL
Lần lấy 1: Xác suất để có bi tím: 10:30 = 1/3
Lần lấy 2: Xác suất để có bi tím: 9:29
Lần lấy 3: Xác suất để có bi tím: 8:28 = 2/7
=> Xác suất để có cả 3 bi tím: 1/3 x 9/29 x 2/7 = 18/609
Mình không chắc có đúng không, bạn kiểm tra hộ mình nhé
Khi nào rảnh vào kênh H-EDITOR xem vid nha!!! Thanks!

Câu 1:
Khong gian mẫu: \(C_{11}^3\)
Có 5 cặp bi cùng số, do đó có \(5\) cách chọn ra 1 cặp cùng số, viên còn lại có 9 cách chọn \(\Rightarrow\) có 45 cách chọn 3 viên có 2 viên cùng số (tất nhiên là ko thể 3 viên cùng số được)
Xác suất: \(P=\frac{C_{11}^3-45}{C_{11}^3}=\frac{8}{11}\)
Câu 2:
Không gian mẫu: \(9!\)
Xếp 4 bạn nam cạnh nhau và hoán vị, có \(4!\) cách
Coi 4 bạn nam này là 1 người, xếp hàng cùng 5 bạn nữ \(\Rightarrow\) có \(6!\) cách hoán vị
Vậy có \(4!.6!\) cách
Xác suất: \(P=\frac{4!.6!}{9!}=\frac{1}{21}\)

Đáp án là B
Tổng số bi lấy ra có 4 viên mà bi đỏ nhiều hơn bi vàng nên có 2 trường hợp xảy ra:
TH1: Không có bi vàng, khi đó số bi đỏ phải từ 1 viên trở lên.
Số cách lấy 4 viên bi bất kì trong tổng số 9 viên bi (gồm 5 đỏ và 4 xanh) là: C 9 4 cách.
Số cách lấy 4 viên bi xanh ( khi đó bi đỏ không được lấy ra) là: C 4 4 cách.
⇒ Số cách lấy thỏa mãn trong trường hợp này là: C 9 4 - C 4 4 = 125 cách.
TH2: Có 1 viên bi vàng, khi đó số bi đỏ phải từ 2 viên trở lên.
Số cách lấy 1 viên bi vàng: C 3 1 cách.
Số cách lấy 3 viên bi còn lại trong đó có 2 bi đỏ và 1 bi xanh là: C 5 2 . C 4 1 cách.
Số cách lấy 3 viên bi còn lại đều là bi đỏ là: C 5 3 . C 4 0 cách.
⇒ Số cách lấy thỏa mãn trong trường hợp này là: C 3 1 . ( C 5 2 . C 4 1 + C 5 3 . C 4 0 ) = 150 cách.
Vậy có 125 + 150 = 275 cách lấy thỏa mãn yêu cầu bài toán.

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Các trường hợp lấy được 4 bi trong đó số bi đỏ lớn hơn số bi vàng như sau:
*TH1: Số bi lấy được không có bi vàng:
- lấy 4 bi đỏ: Có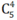 cách
cách
- Lấy 1 bi đỏ, 3 bi xanh có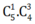 cách.
cách.
- Lấy 2 bi đỏ, 2 bi xanh có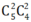 cách.
cách.
- Lấy 3 bi đỏ, 1 bi xanh có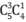 cách.
cách.
*TH2: 4 bi lấy được có đúng 1 bi vàng
- Lấy 2 bi đỏ, 1 bi vàng, 1 bi xanh có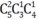 cách.
cách.
- Lấy 3 bi đỏ, 1 bi vàng có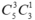 cách.
cách.
Vậy số cách là:
Chọn B.